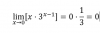-
bb99
el 27/5/19 -
Isabel
el 27/5/19 -
Ana
el 27/5/19
Buenos días! Tengo una duda con este problema de superficie generada al girar la parte positiva alrededor de eje OX y volumen de f(x) al girar alrededor de OY. Y el problema lo tengo por la función que me dan, que es e^(-y)=-x (e elevado a menos y igual a menos x)
Cuando intento hallar f(x), me sale y=-ln(-x), por tanto para x>0 no existiría ningún valor. No sé dónde esta el fallo... =(
Me podéis ayudar? GRACIAS!!
Antonius Benedictus
el 27/5/19¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 27/5/19Vamos con una orientación.
Tienes la ecuación cartesiana implícita de la gráfica de la función:
e-y = -x,
y observa que el primer miembro toma valores estrictamente positivos, por lo que tienes que la variable independiente (x) debe tomar valores estrictamente negativos para que la ecuación sea válida, por lo que tienes que el dominio de la función es:
D = (-∞,0).
Luego, compones en ambos miembros de la ecuación de tu enunciado con la función logarítmica natural, y queda:
-y = ln(-x), aquí multiplicas por -1 en ambos miembros, y queda:
y = -ln(-x),
que es la ecuación cartesiana explícita de la función, y observa que es válida para el dominio que hemos establecido,
y observa además que la imagen de la función es el conjunto de los números reales, por lo que queda expresada:
I = (-∞,+∞).
Luego, planteas la condición para que la función tome valores positivos:
y ≥ 0, sustituyes la expresión remarcada en el primer miembro, y queda:
-ln(-x) ≥ 0, multiplicas en ambos miembros por -1, y queda:
ln(-x) ≤ 0, compones en ambos miembros con la función exponencial natural, y queda:
-x ≤ 1, multiplicas por -1 en ambos miembros, y queda:
x ≥ -1,
por lo que tienes que el intervalo de positividad del dominio de la función es:
Dp = [-1,0).
Luego, planteas la expresión del volumen de revolución de la gráfica de la función (para su trazo positivo) alrededor del eje OX, y queda:
Vx = π*-1∫0 ( -ln(-x) )2*dx = π*-1∫0 ( ln(-x) )2*dx,
que es una integral con su límite superior impropio (te dejo la tarea de plantearla y resolverla).
Luego, planteas la expresión del volumen de revolución de la gráfica de la función (para su trazo positivo) alrededor del eje OY, y queda:
Vy = π*0∫+∞ ( -e-y )2*dy = π*0∫+∞ e-2y*dy,
que es una integral con su límite superior impropio (te dejo la tarea de plantearla y resolverla).
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Laura
el 27/5/19 -
Ivan Moreno
el 27/5/19Buenos días,
Espero que mi duda pueda servir para otras personas en mi situación. Hace unos años decidí meterme
en una carrera, en mi caso ADE, solo que a distancia trabajando "ocho" horas diarias.Esto no seria un problema si no hubiese sido nulo en matemáticas durante toda la ESO y Bachillerato, teniendo como profesor un licenciado sin una pizca de sentido pedagógico, y habiendo dejado un espacio de casi 8 años desde que acabé el Bachillerato Social.
Como creo que este caso cada vez es más frecuente entre personas que deciden ponerse a estudiar despues de un tiempo de haberlo dejado y empezar a estudiar mientras trabajan ¿Que itinerario (módulos) nos/me recomendaríais seguir para conseguir una buena base matemática desde la ESO hasta Bachiller?
Muchísimas gracias de antemano por vuestro tiempo.
Antonius Benedictus
el 27/5/19Tienes que visualizar todos los vídeos de David Calle para esas etapas.
Material de apoyo:
-
Berthin Alexander
el 27/5/19
Breaking Vlad
el 29/5/19 -
Berthin Alexander
el 27/5/19 -
Raul
el 27/5/19 -
José Antonio Alcántara Rosales
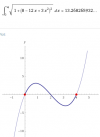
el 27/5/19Por favor necesito ayuda con la longiud de arco de la función x^3-6x^2+8x desde 0 hasta 4 lo he intenté con sustitución trigonometrica pero no no logro despejar x.
Alguien sería tan amable con la respuesta
-
Adrián Garrido Blanco
el 27/5/19limx->0 x*3x-1
Lo he desarrollado:
0*1/3=0/3=0
PEEROO xD Geogebra le da una gráfica con imagen en -1, y en el libro pone que la imagen está en 1
Todo un lío, help me please :)
