-
Jo
el 30/10/18¿De cuantas formas distintas podemos repartir 10 entradas de futbol entre 5 amigos, de forma que cada ´ uno de ellos tenga, al menos, una entrada?
Muchas gracias.
Antonius Benedictus
el 30/10/18
Jo
el 30/10/18 -
Adrian
el 30/10/18 -
Alfonso
el 30/10/18 -
David Poyatos
el 30/10/18Buenas, alguien puede ayudarme con el planteamiento del siguiente problema
Antonio Silvio Palmitano
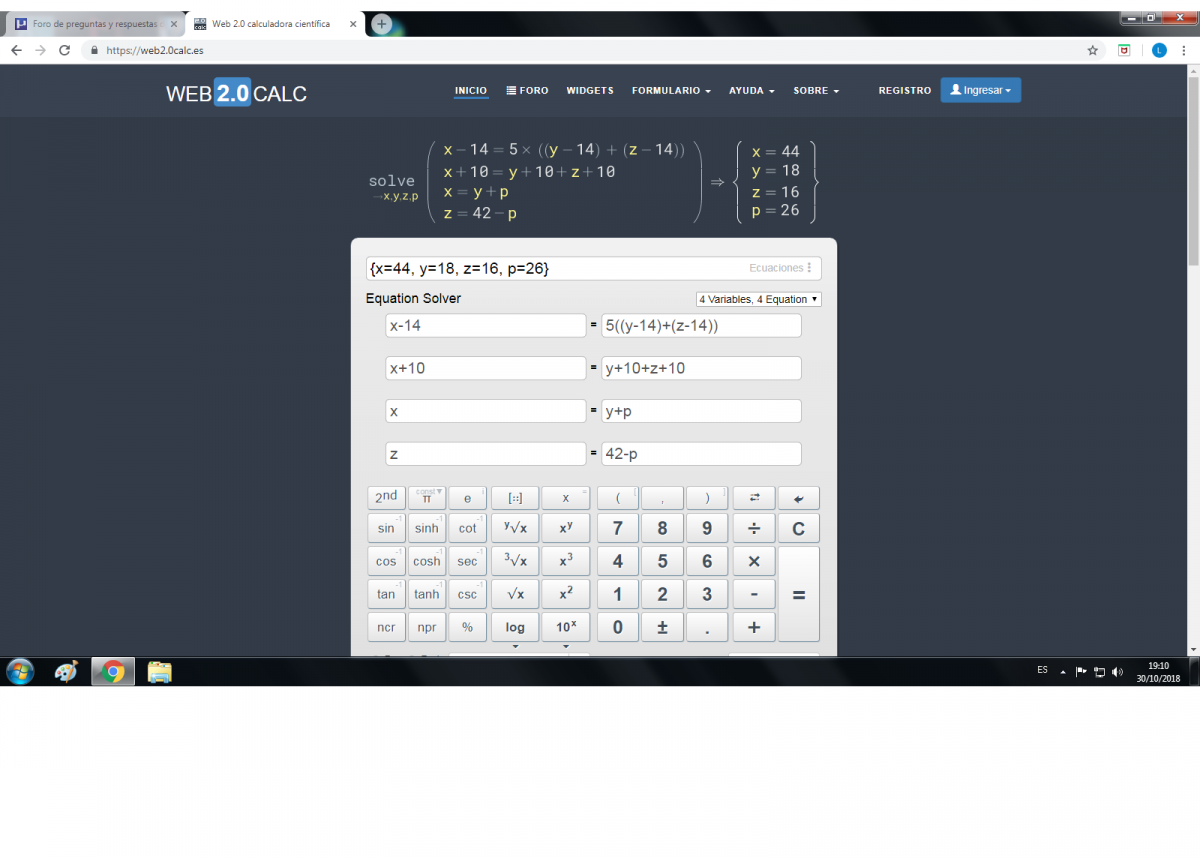
el 31/10/18Puedes llamar x a la edad de la madre, y a la edad del hijo mayor, z a la edad del hijo menor, todas en la actualidad.
Luego, tienes la primera relación de tu enunciado:
"hace 14 años la edad de la madre era igual a 5 veces la suma de las edades de sus hijos",
observa que en esta instancia la edad de la madre era: (x-14), y las edades de los hijos eran: (y-14) y (z-14),
por lo que puedes plantear la ecuación:
x - 14 = 5*( y-14 + z - 14), reduces términos en el agrupamiento, y queda:
x - 14 = 5*(y + z - 28), distribuyes el segundo miembro, y queda:
x - 14 = 5y + 5z - 140, sumas 14 en ambos miembros, y queda:
x = 5y + 5z - 126 (1).
Luego, tienes la segunda relación de tu enunciado:
"dentro de diez años la edad de la madre será igual a la suma de las edades de sus hijos",
observa que en esta instancia la edad de la madre será: (x+10), y las edades de los hijos serán: (y+10) y (z+10),
por lo que puedes plantear la ecuación:
x + 10 = y + 10 + z + 10, restas 10 en ambos miembros, y queda:
x = y + z + 10 (2).
Luego, tienes la tercera relación de tu enunciado:
"cuando el mayor tenga la edad actual de la madre, el menor tendrá 42 años",
observa que si llamas w a la cantidad de años que deben transcurrir para que ocurra esta instancia, tienes que la edad de la madre será: (x+w), y las edades de los hijos serán (y+w) y (z+w),
por lo que puedes plantear las ecuaciones:
y + w = x (3) ("la edad del hijo mayor será igual a la edad actual de la madre"),
z + w = 42 ("la edad del hijo menor será 42 años), aquí restas w en ambos miembros, y queda:
z = 42 - w (4).
Luego, con las ecuaciones señaladas (1) (2) (3) (4) tienes el sistema de cuatro ecuaciones lineales, de primer grado y con cuatro incógnitas:
x = 5y + 5z - 126 (1),
x = y + z + 10 (2),
y + w = x (3),
z = 42 - w (4).
Luego, sustituyes la expresión señalada (3) en las ecuación señalada (1), y queda:
y + w = 5y + 5z - 126, aquí restas y en ambos miembros, y queda:
w = 4y + 5z - 126, aquí sustituyes la expresión señalada (4), y queda:
w = 4y + 5(42 - w) - 126, distribuyes el factor común con su agrupamiento, y queda:
w = 4y + 210 - 5w - 126, sumas 5w en ambos miembros, reduces términos semejantes, y queda:
6w = 4y + 84, restas 4y y restas 6w en ambos miembros, y queda:
-4y = -6w + 84, divides por -4 en todos los términos de la ecuación, y queda:
y = (3/2)w - 21 (5).
Luego, sustituyes la expresión señalada (3) en la ecuación señalada (2), y queda:
y + w = y + z + 10, aquí restas y en ambos miembros, y queda:
w = z + 10, aquí sustituyes la expresión señalada (4), y queda:
w = 42 - w + 10, sumas w en ambos miembros, reduces términos semejantes, y queda:
2w = 52, divides por 2 en ambos miembros, y queda:
w = 26 (6).
Luego, reemplazas el valor remarcado y señalado (6) en la ecuación señalada (5), y queda:
y = (3/2)(26) - 21, resuelves el segundo miembro, y queda:
y = 18 (7).
Luego, reemplazas el valor remarcado y señalado (6) en la ecuación señalada (4), y queda:
z = 42 - 26, resuelves el segundo miembro, y queda:
z = 16 (8).
Luego, reemplazas los valores remarcados y señalados (6) (7) (8) en la ecuación señalada (2), y queda:
x = 18 + 16 + 10, resuelves el segundo miembro, y queda:
x = 44.
Luego, tienes que las edades de las tres personas, ordenadas de mayor a menor son:
44, 18 y 16 (en la actualidad),
30, 4 y 2 (hace catorce años),
54, 28 y 26 (dentro de diez años),
70, 44 y 42 (dentro de 26 años).
Espero haberte ayudado.
-
Laura
el 30/10/18Hola, me ayudarian con esta integral ∫√(1+4/49x2 ) gracias.
-
Usuario eliminado
el 30/10/18 -
carmela
el 30/10/18 -
Skyxot 360
el 30/10/18 -
Usuario eliminado
el 30/10/18Buenos días a todos, estoy un poco insegura con un ejercicio que estoy haciendo de Geometría. ¿Podrían ayudarme a verificar que la solución y el desarrollo es correcto? Gracias y un gran saludo!
Adjunto el ejercicio y la solución:
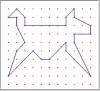
En relación con el polígono irregular adjunto (perro), que se ha trazado en el PPTC (papel punteado de trama cuadrada):
Determina su área mediante el método de adición o descomposición (división del polígono dado en figuras elementales convenientemente construidas y determinación de la suma de las áreas de cada una de ellas). ¿Cómo se denominan los triángulos en la descomposición del polígono: equiláteros, isósceles, escalenos, obtusángulos o rectángulos?
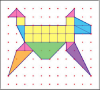
De las muchas descomposiciones posibles del polígono propuesto se ha realizado la siguiente:
a) 6 triángulos rectángulos isósceles de color rosa: A1 = 0,5 (u2) · 6 = 3 (u2). El área de cada uno de ellos es 0,5, por ser la mitad de un cuadrado de área unidad.
b) 4 triángulos rectángulos escalenos de color azul: A2= 1 (u2) · 4 = 4 (u2). El área del conjunto de los triángulos azules es el número racional 4. El área de cada uno de los 4 triángulos azules es 1, pues cualquiera de ellos puede considerarse como la mitad de un rectángulo cuya área es 2.
c) 14 cuadrados unitarios de color amarillo : A3 = 1 (u2) · 14 = 14 (u2)
d) 1 cuadrilátero trapecio color verde: se utilizará el ‘’método de complementación parcial’’. En este caso, se ha considerado que la figura se encuentra inscrita en un rectángulo cuya superficie es de 10 u2, a dicha cifra se le resta la de los dos triángulos isósceles (de color blanco), cuyas respectivas áreas son de 2 y 2 (u2).
A4 = 10 – 2 – 2 = 10 – (2 + 2) = 6
A4= 6 (u2) · 1 = 6 (u2)
e) 1 triángulo rectángulo escaleno de color lila A5= 3 (u2) · 1 = 3 (u2). El área del triángulo es 3, pues puede considerarse como la mitad de un rectángulo cuya área es 6 (la figura se inscribe en un rectángulo compuesto por 4 cuadrados completos y 4 mitades).
f) 1 triángulo obtusángulo escaleno de color naranja: se utilizará el ‘’método de complementación parcial’’. En dicho caso, se ha considerado que la figura está inscrita en un cuadrado cuya superficie es de 9 u2, a dicha cifra se le resta la de los dos triángulos de color blanco, cuyas respectivas áreas son de 4,5 (triángulo isósceles de la derecha) y 1,5 (triángulo rectángulo escaleno de la izquierda) u2.
A6 = 9 – 4,5 – 1,5 = 9 – (4,5 + 1,5) = 3
A6= 3 (u2) · 1 = 3 (u2)
- Resultado: Apolígono = 3 + 4 + 14 + 6 + 3 + 3 = 33 (u2)
-
Zanubia Nufuri
el 30/10/18
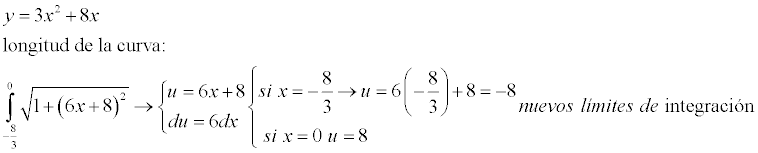
Espero que te sirva!!! :D
