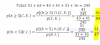-
hola, alguien me ayuda a demostrar esto:
a) Demuestre que la recta perpendicular a la cicloide en cada punto pasa por el punto de tangencia de la circunferencia con el eje x.
b) Demuestre que el radio de curvatura de la cicloide en cualquiera se sus puntos es el doble de la longitud del segmento normal en el mismo punto.
NOTA: se llama segmento normal al segmento perpendicular a la recta tangente desde el punto de tangencia hasta el eje de las abscisas.
muchas gracias, disculpen las molestias
Antonius Benedictus
el 1/11/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Antonio Silvio Palmitano
el 2/11/18Observa que las dos semirrectas de la gráfica de la función cuya expresión cartesiana es:
f(x) = |x| tienen ecuaciones:
y = x (para x ≥ 0), cuya ecuación en coordenadas polares es: θ = π/4 o θ = 9π/4,
y = -x (para x < 0), cuya ecuación en coordenadas polares es: θ = 3π/4 o θ = 11π/4.
Luego, recuerda la expresión del área de una región plana en coordenadas polares:
A = θ1∫θ2 (1/2)*r2*dθ.
Luego, puedes plantear para la expresión del área de la región limitada por las dos semirrectas y la segunda espiral (observa que indicamos con corchetes que debes evaluar con Regla de Barrow):
A2 = 9π/4∫11π/4 (1/2)*r2*dθ = 9π/4∫11π/4 (1/2)*(2θ)2*dθ = 9π/4∫11π/4 2*θ2*dθ = [ (2/3)*θ3 ],
luego evalúas, y queda:
A2 = (2/3)*(11π/4)3 - (2/3)*(9π/4)3 =
= (2/3)*(1331π3/64) - (2/3)*(729π3/64) =
= (2/3)*(602π3/64) =
= 301π3/48.
Luego, puedes plantear para la expresión del área de la región limitada por las dos semirrectas y la primera espiral (observa que indicamos con corchetes que debes evaluar con Regla de Barrow):
A1 = π/4∫3π/4 (1/2)*r2*dθ = π/4∫3π/4 (1/2)*(2θ)2*dθ = π/4∫3π/4 2*θ2*dθ = [ (2/3)*θ3 ],
luego evalúas, y queda:
A2 = (2/3)*(3π/4)3 - (2/3)*(π/4)3 =
= (2/3)*(27π3/64) - (2/3)*(π3/64) =
= (2/3)*(26π3/64) =
= 13π3/48.
Luego, puedes plantear para la expresión del área de la región comprendida entre las dos semirrectas y las dos espirales:
A = A2 - A1 = reemplazas valores = 301π3/48 - 13π3/48 = 288π3/48 = simplficas = 6π3.
Espero haberte ayudado.
-
Antonio
el 1/11/18p(t)=10000/(1+19e-t/5)
v(t)=p'(t)=38000e-t/5/(1+19e-t/5)2
v(1)=38000e-1/5/(1+19e-1/5)2=113.50
v(10)=38000e-10/5/(1+19e-10/5)2=403.20
v'(t)=7600e-t/5(19e-t/5-1)/(1+19e-t/5)3
v'(t)=0=>7600e-t/5(19e-t/5-1)/(1+19e-t/5)3=0=>7600e-t/5(19e-t/5-1)=0=>19e-t/5-1=0=>
=>19e-t/5=1=>-t/5=ln(1/19)=>t=-5ln(1/19)=14.72
v(14.72)=38000e-14.72/5/(1+19e-14.72/5)2=499.99