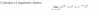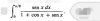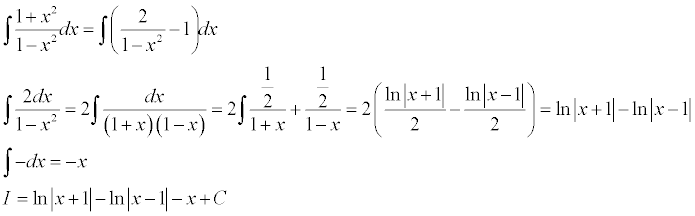-
Ayuden, nos sean malos. .-.
Antonio Silvio Palmitano
el 2/11/181°)
La función está definida en el punto en estudio: f(0,0) = 0 (1).
2°)
Planteas su derivada parcial con respecto a x en el punto en estudio, y queda:
fx(0,0) = Lím(h→0) ( f(0+h,0) - f(0,0) )/h = sustituyes expresiones y cancelas términos nulos:
= Lím(h→0) h*sen(0)/h2 = Lím(h→0) 0/h2 = 0 (2).
3°)
Planteas su derivada parcial con respecto a x en el punto en estudio, y queda:
fy(0,0) = Lím(k→0) ( f(0,0+k) - f(0,0) )/k = sustituyes expresiones y cancelas términos nulos:
= Lím(k→0) 0*sen(0)/k2 = Lím(k→0) 0/k2 = 0 (3).
4°)
Planteas la ecuación de diferenciabilidad, y queda:
f(0+h,0+k) = f(0,0) + fx(0,0)*h + fy(0,0) + ε(h,k)*(h2+k2)1/2,
sustituyes expresiones y valores, cancelas términos nulos, y queda:
h*sen(h*k)/(h2+k2) = ε(h,k)*(h2+k2)1/2,
divides en ambos miembros por , y queda:
h*sen(h*k)/(h2+k2)3/2 = ε(h,k) (4).
5°)
Planteas el límite para h y k tendiendo a cero de la función cuya expresión está señalada (4), y queda:
L = Lím( (h,k)→(0,0) ) ε(h,k) = sustituyes la expresión señalada (4), y queda:
= Lím( (h,k)→(0,0) ) h*sen(h*k)/(h2+k2)3/2 = indeterminado;
luego, a fin de estudiar su existencia o no existencia, puedes plantear la familia de trayectorias rectas cuya ecuación es:
k = mh, sustituyes esta expresión en el argumento del límite, y queda:
L = Lím(h→0) h*sen(m*h2)/( h2*(1+m2) )3/2 = distribuyes la potencia en el denominador, y queda:
= Lím(h→0) h*sen(m*h2)/( h3*(1+m2)3/2 ) = simplificas, y queda:
= Lím(h→0) sen(m*h2)/( h2*(1+m2)3/2 ) = extraes el factor constante, y queda:
= ( 1/(1+m2)3/2 )*Lím(h→0) sen(m*h2)/h2 =
multiplicas por m al numerador y al denominador del argumento del límite, extraes el factor constante, y queda:
= ( m/(1+m2)3/2 )*Lím(h→0) sen(m*h2)/(m*h2) =
luego, observa que el límite es igual a uno (revisa tus apuntes de tu curso anterior de cálculo), por lo que queda:
= ( m/(1+m2)3/2 )*1 =
= m/(1+m2)3/2,
que es una expresión que depende de las pendientes de las rectas de la familia de trayectorias, por lo que tienes que este límite no existe, y puedes concluir que la función no es diferenciable en el punto en estudio: (0,0).
Espero haberte ayudado.
-
Buenas tardes,
Teniendo esto he encontrado que la derivada de la función da 0, por lo tanto esto qué significa? qué la función es constante de 0 a infinito sin crecimiento ni decrecimiento?
Si es así como se expresaría esto correctamente? gracias.
Antonio Silvio Palmitano
el 2/11/18Observa que puedes expresar a la raíz como una potencia con exponente fraccionario, y queda:
f(x) = x1/lnx,
y observa que la función tampoco está definida para x = 1, porque se anula el denominador del exponente de la expresión para este valor;
luego, expresas a la base de la potencia como un exponencial, y queda:
f(x) = (elnx)1/lnx,
aplicas la propiedad de la potencia cuya base es otra potencia, simplificas en el exponente, y queda:
f(x) = e.
Luego, tienes que la expresión de la función es constante en todo su dominio: D = (0,1)∪(1,+∞).
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 2/11/1810)
Tienes un sistema de tres ecuaciones lineales, de primer grado y con tres incógnitas, y el determinante de la matriz del sistema es:
D =
a 1 1
1 a 1
1 1 a;
desarrollas el determinante, y queda:
D = (a3+1+1)-(a+a+a) = a3-3a+2.
Luego, planteas la condición para que el sistema sea compatible indeterminado o incompatible, y queda la ecuación:
D = 0, sustituyes la expresión del determinante, y queda:
a3 - 3a + 2 = 0,
que es una ecuación polinómica cúbica, observa que a = 1 es una de sus raíces, por lo que puedes factorizar con la Regla de Ruffini, y queda:
(a - 1)*(a2 +a - 2) = 0,
luego, factorizas el polinomio cuadrático del segundo factor por medio de la fórmula resolvente, y queda:
(a - 1)*(a - 1)*(a + 2) = 0,
reduces factores semejantes, y queda:
(a - 1)2*(a + 2) = 0;
luego, por anulación de una multiplicación, tienes dos opciones:
(a - 1)2 = 0, de donde puedes despejar: a = 1,
a + 2 = 0, de donde puedes despejar: a = -2.
Luego, ya puedes concluir que el sistema es compatible determinado y admite una única solución
para a ≠ 1 y a ≠ -2.
Luego, pasamos a considerar el sistema de tu enunciado para cada uno de los valores remarcados:
a)
Para a = 1, observa que las tres ecuaciones quedan iguales a:
x + y + z = 1, aquí restas x y restas y en ambos miembros, y queda:
z = 1 - x - y, por lo que tienes que el sistema es compatible indeterminado y admite infinitas soluciones, que quedan expresadas:
x ∈ R,
y ∈ R,
z = 1 - x - y.
b)
Para a = -2, aplicamos el Método de Gauss, a partir de la matriz ampliada del sistema, que queda:
-2 1 1 1
1 -2 1 1
1 1 -2 1;
permutas la primera fila con la tercera, y queda:
1 1 -2 1
1 -2 1 1
-2 1 1 1;
a la segunda fila le restas la primera, a la tercera fila le sumas el doble de la primera, y queda:
1 1 -2 1
0 -3 3 0
0 3 -3 3;
a la segunda fila la multiplicas por -1/3, a la tercera fila la multiplicas por 1/3, y queda:
1 1 -2 1
0 1 -1 0
0 1 -1 1;
a la tercera fila le restas la segunda fila, y queda:
1 1 -2 1
0 1 -1 0
0 0 0 1;
que es una matriz escalonada;
luego, planteas el sistema de ecuaciones equivalente, y queda:
x + y - 2z = 1,
y - z = 0,
0 = 1,
y observa que tienes una identidad falsa en el lugar de la tercera ecuación del sistema, por lo que puedes concluir que el sistema es incompatible y no admite solución.
Espero haberte ayudado.
-
Buenos días lo siguiente es de estadistica y probabilidades, os pongo la pregunta y la respuesta, lo que necesito es la explicación porque no me entero, muchas gracias por vuestra ayuda
PREGUNTA: Una caja de galletas tiene 25 de chocolate, 35 de mantequilla y 20 de fruta confitada.
Una persona saca, aleatoria y consecutivamente, 3 galletas de la caja y se las come.
1) Hallar la probabilidad de que el orden de elección sea de fruta confitada, de mantequilla
y de chocolate.
2) Hallar la probabilidad de que las tres galletas sean de chocolate.
RESPUESTA:
Antonio Silvio Palmitano
el 2/11/18a)
Elige la primera galleta (observa que tiene 20 de fruta y 80 en total), y la probabilidad es: 20/80.
Luego, elige la segunda galleta (observa que tiene 35 de mantequilla y 79 en total, porque ya se ha comido una), y la probabilidad es: 35/79.
Luego, elige la tercera galleta (observa que tiene 20 de chocolate y 78 en total, porque ya se ha comido dos), y la probabilidad es: 20/78.
Luego, como para cada elección posible de la primera galleta tiene otras opciones para elegir la segunda, y por cada opción tiene otras para elegir la tercera, aplicas el Principio de Multiplicación, y queda:
p = (20/80)*(35/79)*(20/78).
b)
Elige la primera galleta (observa que tiene 25 de chocolate y 80 en total), y la probabilidad es: 25/80.
Luego, elige la segunda galleta (observa que tiene 24 de mantequilla y 79 en total, porque ya se ha comido una), y la probabilidad es: 24/79.
Luego, elige la tercera galleta (observa que tiene 23 de chocolate y 78 en total, porque ya se ha comido dos), y la probabilidad es: 23/78.
Luego, como para cada elección posible de la primera galleta tiene otras opciones para elegir la segunda, y por cada opción tiene otras para elegir la tercera, aplicas el Principio de Multiplicación, y queda:
p = (25/80)*(24/79)*(23/78).
Espero haberte ayudado.
-
¿Alguien me puede explicar como resolver este limite? He probado l'Hôpital, pero no he conseguido hallar la respuesta, en teoría debe de dar e^-π, entiendo de donde podría salir la e pero el -π no. Gracias.