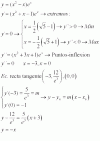-
Antonio
el 28/10/18Sea x, y y z la rentabilidad respectivamente a los modelos A, B, C
El primero obtiene una rentabilidad de 5000x+25000y+25000z pero también es el 15% de (5000+25000+25000)
El segundo obtiene una rentabilidad de 12500x+25000y+12500z pero también es el 12% de (12500+25000+12500)
El primero obtiene una rentabilidad de 10000x+10000y+20000z pero también es el 10% de (10000+10000+20000)
construyendo un sistema:
5000x+25000y+25000z=15000
12500x+25000y+12500z=6000
10000x+10000y+20000z=4000
resolviendo el sistema
x=23/100=23%
y=11/100=11%
z=3/100=3%
la rentabilidad es 23%, 11% y 3% respectivamente
-
Hola, no sé cómo empezar a hacer este ejercicio, ¿alguien me podría ayudar a plantear el principio? El ejercicio es:
Si g(x) es continua en x=0, demuestra que f(x)=xg(x) es derivable en x=0 y halla f ‘ (0).
Muchas gracias.
-
Muchas Gracias Raul? Mi suscripción es pro ,no entiendo que no haya mas vídeos aquí que en you tube.¿Saben como me puedo poner en contacto con algún responsable?
-
Antonio
el 28/10/18y=(x2-x)ex
y'=(2x-1)ex+(x2-x)ex=(x2+x-1)ex
y''=(2x+1)ex+(x2+x-1)ex=(x2+3x)ex
y''=0 => (x2+3x)ex=> x2+3x=0 => x1=0 ^x2=-3
tenemos por lo tanto dos puntos de inflexión x1=0 ^x2=-3
(-inf,-3) es cóncava pues la segunda derivada es positiva
(-3,0) es convexa pues la segunda derivada es negativa
(0,+inf) es cóncava pues la segunda derivada es positiva
-
Hola ,buenos ,Días! Soy un padre con una hija en tercero de ESO,acabo de hacer la suscripción y no encuentro vídeos de áreas y volúmenes ,me sale lo mismo que esta colgado en you tube.¿ Alguien me puede ayudar por favor ?
-
Alguien me puede ayudar con este ejercicio?
X3 -5x2 +6x > 0
Antonio
el 28/10/18