-
Raquel Gonzalez
el 27/8/18Hola!, espero me puedan ayudar con este ejercicio, en serio que no he podido resolverlo :c.
Si el largo de unos pernos es una variable aleatoria X que sigue un modelo normal de media 11 cms. Y una varianza de 4cms^2. El fabricante separa los pernos en tres categorias: A, B Y C, en donde C es mayor a 12 cm. Si se mantiene la varianza ¿cuanto valdrá la longitud media si la categoría C de los pernos constituyen el 25 % de la producción total? -
Sofía
el 27/8/18Cómo hago para hallar un número racional y otro irracional comprendidos entre 2,236 y √5? Gracias!
Antonio Silvio Palmitano
el 27/8/18Tienes los números reales:
a = 2,236 = 2,236000,
b = √(5) = 2,236068... (recuerda que los puntos suspensivos indican que continúan indefinidamente las cifras decimales).
Luego, puedes plantear el número racional:
x = 2,236010, y observa que es un número con ses cifras decimales, por lo que tienes que x es un número racional que es mayor que a y menor que b.
Luego, puedes disminuir una de las tres últimas cifras decimales de las que hemos consignado para el número b, y por ejemplo tienes:
y = 2,236058... , y observa que es un número con infinitas cifras decimales, y que no es periódico, por lo que tienes que y es un número irracional que es mayor que a y es menor que b.
Espero haberte ayudado.
-
Mario M
el 26/8/18Ejercicio 1, apartado w: log2 (-16) =?
-
Ainhoa Ramos
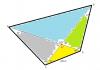
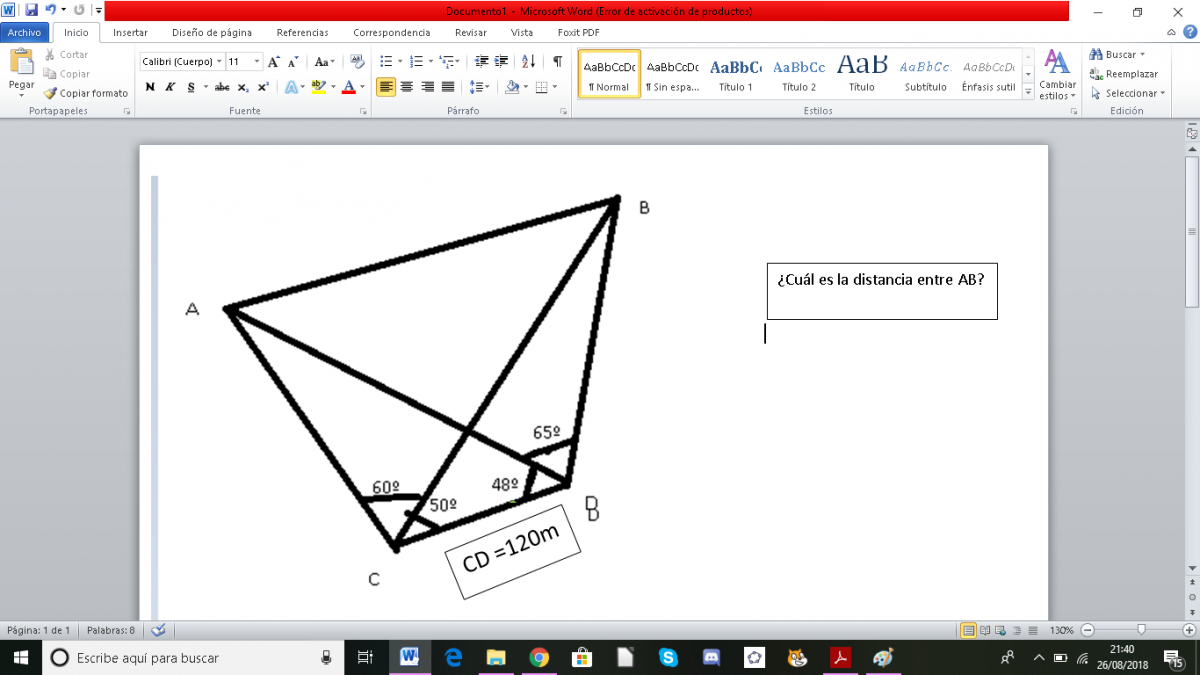
el 26/8/18A mi me dio que AB = 330,86m, no se si está bien
Antonio Silvio Palmitano
el 27/8/18
Observa que es muy sencillo calcular la medida del ángulo central del triángulo amarillo: 180° - 50° - 48° = 82°. Luego, recuerda que para los demás ángulos centrales, tienes que su opuesto por el vértice mide también 82° (en el triángulo celeste), y los otros dos son suplementarios: 180° - 82° = 98° (uno en el triángulo verde y otro en el triángulo violeta).
Luego, con el mismo procedimiento, puedes calcular las medidas de los ángulos restantes en el triángulo violeta y en el triángulo verde, y observa que ya hemos indicado cuáles son sus medidas.
Luego, puedes plantear el problema por etapas:
1°)
en el triángulo amarillo, aplicas el Teorema del Seno, y tienes dos ecuaciones:
a)
sen(48°)/CP = sen(82°)/CD, de aquí despejas: CP = sen(48°)*CD / sen(82°), reemplazas valores, resuelves, y queda: CP ≅ 90,054 m (1);
b)
sen(50°)/DP = sen(82°)/CD, de aquí despejas: DP = sen(50°)*CD / sen(82°), reemplazas valores, resuelves, y queda: DP ≅ 92,829 m (2).
2°)
en el triángulo violeta, aplicas el Teorema del Seno, y tienes la ecuación:
sen(60°)/AP = sen(22°)/CP, de aquí despejas: AP = sen(60°)*CP/sen(22°), reemplazas valores, entre ellos el valor señalado (1), resuelves, y queda:
AP ≅ 208,189 m (3);
3°)
en el triángulo verde, aplicas el Teorema del Seno, y tienes la ecuación:
sen(17°)/DP = sen(65°)/BP, de aquí despejas: BP = sen(65°)*DP/sen(17°), reemplazas valores, entre ellos el valor señalado (2), resuelves, y queda:
BP ≅ 287,756 m (3);
4°)
en el triángulo celeste, aplicas el Teorema del Coseno, y tienes la ecuación:
AB2 = AP2 + BP2 - 2*AP*BP*cos(82°),
reemplazas valores, resuelves en cada término, y queda:
AB2 ≅ 43342,660 + 82803,516 - 16675,062,
resuelves el segundo miembro, y queda:
AB2 ≅ 109471,114,
extraes raíz cuadrada en ambos miembros, y queda:
AB ≅ 330,864 m;
y observa que por medio del Teorema del Seno, puedes calcular las medidas de los ángulos agudos restantes del triángulo celeste.
Espero haberte ayudado.
-
Ainhoa Ramos
el 26/8/18Podrían llegar a penalizarme un ejercicio de un examen por nombrar a lo que me piden de forma diferente? por ejemplo, cuando se trata de la trigonometría, imaginense que yo nombro a los ángulos siguiendo el orden dado por las agujas del reloj, pero el profesor lo nombra en sentido contrario y lo que a mi me dio en el lado correspondiente a la "c", al profesor le sale en el lado "b".
-
Sofía
el 26/8/18En la demostración de que √5 es irracional se parte suponiendo que es racional, es decir, que se puede expresar como un cociente de números enteros (a/b), pero llegado un punto del desarrollo queda algo así: 5b² = a² , entonces a² es múltiplo de 5 porque se puede obtener mediante 5b², y debo suponer que si a² es múltiplo de 5, entonces a también es múltiplo de 5. Entonces se me ocurrió buscar un número b que elevado al cuadrado y multiplicado por 5 de otro número elevado al cuadrado, pero no encontré ninguno, es decir, no encontré un a. Por ejemplo, suponiendo que b = 5, b² =5² =25, entonces 5b² = 5×25 = 125 que sería a², pero la raíz de 125 es 11.18033989... que sería a, pero ese número es un múltiplo de 5? Y pasa lo mismo con todos los demás números enteros que elija. Nada parece tener mucho sentido.
Se que debería haber seguido con la suposición de que si a² es múltiplo de 5 entonces a también lo es para terminar con la demostración, pero esto me parece muy curioso y quiero entenderlo o saber si estoy equivocada en algo.
Gracias!
Antonio Silvio Palmitano
el 27/8/18Observa que en tu demostración se comienza a partir de un Supuesto Absurdo: √(5) es un número racional.
Por lo tanto, puedes plantear que existe un número fraccionario no simplificable a/b que cumple con la igualdad:
a/b = √(5), aquí elevas al cuadrado en ambos miembros, y queda:
a2/b2 = 5, aquí multiplicas por b2 en ambos miembros, y queda:
a2 = 5*b2 (1),
por lo que tienes que a2 es un múltiplo de cinco, por lo que tienes entonces que el número natural a es múltiplo de cinco, y entonces tienes que existe un número natural x que cumple la igualdad:
a = 5*x (2);
luego, sustituyes la expresión señalada (2) en la igualdad señalada (1), y queda:
(5*x)2 = 5*b2, aquí distribuyes la potencia entre los dos factores de su base en el primer miembro, y queda:
25*x2 = 5*b2, aquí divides por cinco en ambos miembros, y queda:
5*x2 = b2 (2),
por lo que tienes que b2 es un múltiplo de cinco, por lo que tienes entonces que el número natural b es múltiplo de cinco, y entonces tienes que existe un número natural y que cumple la igualdad:
b = 5*y (3).
Luego, vuelves al supuesto absurdo del comienzo, y tienes:
√(5) = a/b, donde este número fraccionario que no es simplificable;
luego, sustituyes las expresiones señaladas (2) (3), y queda:
√(5) = 5*x / 5*y,
y observa que la expresión del segundo miembro corresponde a un número fraccionario que es simplificable por cinco;
y como esta conclusión contradice el supuesto absurdo, entonces puedes afirmar que no existe un número fraccionario que sea igual a √(5) y, por lo tanto, tienes que √(5) no pertenece al conjunto de los números racionales.
Espero haberte ayudado.
-
Denisa M?d?lina Florean
el 26/8/18 -
Patricia
el 26/8/18Necesito vuestra ayuda otra vez.
No sabemos resolver el ejercicio!!
Izan Beltrán
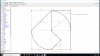
el 26/8/18Si miramos cada cuadrado tal que así:
No sé si te piden el área blanca o la negra, yo voy a calcular la blanca:Cuadrado 1) El área blanca correspone a 1/4 del área de un círculo de radio 2: pi x 22 / 4 = pi
Cuadrado 2) 3/4 del cuadrado: 3/4 x 22 = 3
Cuadrado 3) 1/2 del cuadrado: 1/2 x 22 = 2
Cuadrado 4) El área del cuadrado menos 1/4 del área de un círculo de radio 2 (que antes hemos visto que es igual a pi): 22 - pi
Total) pi + 3 + 2 + 22 - pi = 3 + 2 + 4 = 9
Ya que el área blanca es 9, vamos a calcular la negra, que es la total menos la blanca: 42 - 9 = 7
Este es el método, y parece que esta vez el solucionario es correcto y pide el área negra jaja. Espero que os ayude.
-
Cristina
el 26/8/18
