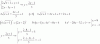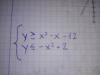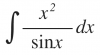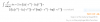-
Ruben Gonzalez Lorenzo
el 29/8/18Buenas a todos.
Me gustaria saber si alguien me puede ayudar con este problema de probabilidad
La edad de un determinado grupo de personas sigue una distribución N(35, 10). Calcula la probabilidad de que una persona de ese grupo, elegido al azar, tenga:
a) Más de 40 años.
b) Entre 23 y 47 años.
c) Si en el grupo hay 500 personas,¿cuantas de ellas se puede esperar que sean mayores de 40 años?
bB9
Mi duda reside en el apartado c,que no se muy bien como lantaearlo.Seria una binomial B(500,0´3),siendo 0,3 el resultado del apartado A),y se aproxima a una normal?
Gracias y un saludo¡¡
Antonius Benedictus
el 29/8/18 -
Álvaro Terrasa
el 29/8/18
Buenas! Tengo este sistema de ecuaciones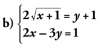
El caso es que yo lo he hecho de esta manera
Y se supone que los resultados me tienen que salir x1 = -1, x2 = 8, y1 = -1 e y2 = 5.
Sinceramente, he mirado bien el procedimiento y no veo el fallo. Si alguien me pudiera señalar cual es el fallo, me haría un gran favor.
-
Paula
el 29/8/18Hola chicos, soy Paula de Uruguay y estoy terminando el bachillerato en Administración. Hoy tuve un escrito de Mat. A y se me mezclaron las neuronas ya que no tenía ningún ejercicio parecido
Había que realizar el E.A. y R.G. de f(x) =(-x +2) e x-1/x
¿Hay algún video que tenga el -x ? Gracias, son los mejores. Saludos
-
Jordi García
el 29/8/18Hola UNICOOS,
Tengo que estudiar la curvatura (concavidad, convexidad y puntos de inflexión) de la siguiente función:
f(x) = 1/(x2- 4)
El problema que tengo es que la función no presenta puntos de inflexión porque la segunda derivada siempre es positiva y, por tanto, no tiene raíces. ¿Cómo estudio la concavidad y convexidad? ¿La función es convexa en todo su dominio? Al visualizarla en GeoGebra no es así, es como que no tiene curvatura porque todos los extremos tienden a ∞ debido a sus asíntotas. ¿Qué tengo que poner?
Gracias.
César
el 29/8/18Jordi García
el 29/8/18Hola César, gracias por contestar, tu comentario me ha hecho ver en qué he fallado:
f''(x) ≠ 0 → no existen puntos de inflexión
Sin embargo, f''(x) sí que puede ser negativa... Al estudiar la curvatura tenemos que estudiar el signo de f''(x) en los intervalos que limitan, además de las raíces de f''(x), los puntos de discontinuidad. Raíces no tiene, pero puntos de discontinuidad sí, -2 y 2.
Entonces la solución me sale:
f(x) es convexa en (-∞, -2) ∪ (2, ∞)
f(x) es cóncava en (-2, 2)
-
José Carlos
el 29/8/18
Buenas, ¿cómo se resuelve la segunda parte del ejercicio que pide aproximar el desarrollo de Fourier de f(x)=x a la series que indica? (1/n² ó 1-1/3+1/5...)
Gracias
Antonius Benedictus
el 29/8/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Jesus Angel Rodriguez
el 29/8/18que pasos tengo que seguir para resolver esta inecuacion.
Jesus Angel Rodriguez
el 29/8/18 -
JUAN AMPIE
el 29/8/18 -
juan sebastian vega
el 29/8/18 -
Diego Mauricio Heredia
el 29/8/18 -
DAVID
el 28/8/18Encuentra la ecuación de la recta que pase por A(-2,-1) y sea periódica a la recta que pasa por B(2,1) y C(1,5).
Escribe la ecuación general y la explícita
Diaz Daniel Victor
el 28/8/18Hola David, creo que no existen la rectas periódicas con otras rectas, porque sino se tocarían cada cierta distancia y eso obliga a que no sea una recta sino una curvilínea... puse las fórmulas para que puedas ver de dónde saco cada cosa... recordá que cada par ordenado está formado por una coordenada en x que aparece primero, también por otra coordenada en y, a la hora de reemplazar podés cualquiera en cualquier fórmula pero siempre las de las Y con las Y, para las X también X con X
PD: supuse que donde dice periódica debería decir paralela o perpendicular
