-
Por favor ayúdame con el inciso a) del siguiente ejercicio que no me da la respuesta. Muchas gracias. R/ a) 0.333 m/s, 3.33 Joules
Los bloques A (masa 2 kg) y B (masa 10 kg) se mueven en una superficie horizontal sin fricción. En un principio, el bloque B esta en reposo y el A se mueve hacia él a 2 m/s. Los bloques están equipados con protectores de resorte ideal. El choque es de frente, así que todos los movimientos antes y después del choque están en una linea recta. a) Calcule la energía máxima almacenada en los protectores de resorte y la velocidad de cada bloque en ese momento. b) Calcule la velocidad de cada bloque una vez que se han separado.
Raúl RC
el 10/11/18carlos
el 10/11/18Antonio Silvio Palmitano
el 10/11/18Observa que la velocidad del centro de masas, calculada con los valores antes del choque, queda:
Vcm = (2*2+10*0)/(2+10) = 4/12 = 1/3 m/s ≅ 0,333 m/s,
y es la velocidad que tienen los dos bloques mientras están juntos, y los resortes se encuentran comprimidos.
Observa que la energía mecánica total del sistema, calculada con los valores antes del choque (observa que los resortes en este caso se encuentran relajados), queda:
EMT = (1/2)*2*22 + (1/2)*10*02 = 4 + 0 = 4 J (1),
y observa que esta energía mecánica (antes del choque) está asociada al bloque A, porque el bloque B se encuentra en reposo, por lo que puedes plantear que la energía mecánica (en realidad solo cinética) del bloque A es:
EMAi = 4 J.
Luego, tienes que en el instante en el que los bloques están comprimidos, la velocidad del bloque A (y también del bloque B) es la velocidad del centro de masas del sistema, por lo que en dicho instante, tienes que la energía mecánica del bloque A (durante el choque) es:
EMAc = (1/2)*2*(1/3)2 = 1/9 J (2).
Luego, tienes que en el instante en el que los bloques están comprimidos, la velocidad del bloque B (y también del bloque A) es la velocidad del centro de masas del sistema, por lo que en dicho instante, tienes que la energía mecánica del bloque B (durante el choque) es:
EMBc = (1/2)*10*(1/3)2 = 5/9 J (3).
Luego, puedes llamar EMr a la energía almacenada en los resortes durante el choque, y como la energía mecánica se conserva, puedes plantear que la suma de las energías durante el choque es igual a la energía mecánica total, por lo que puedes plantear la ecuación:
EMAc + EMBc + EMr = EMT,
remplazas los valores señalados (2) (3) (1), y queda:
1/9 + 5/9 + EMr = 4,
reduces términos semejantes en el primer miembro, y queda:
2/3 + EMr = 4,
restas 2/3 en ambos miembros, y queda:
EMr = 10/3 J ≅ 3,333 J.
Espero haberte ayudado.
-
Me podrían ayudar con la pregunta a y b de este ejercicio. Muchas gracias.

Raúl RC
el 9/11/18a) El campo electrico lo podemos obtener a partir de la diferencia de potencial mediante la expresion:
E=ΔV/d siendo d=x2-x1=12 cm=0,12 m
Por tanto E=-240/0,12=-2000 V/m
En forma vectorial: E=-2000i V/m
b) Con el calculo del campo electrico podemos hallar la nueva diferencia de potencial con la expresion anterior:
E=ΔV/d=>ΔV=E·d=-2000·0,14=-280 V
Mejor?
-
Raúl RC
el 9/11/18Tienes resuelto en este link un ejercicio idéntico, échale un ojo
http://www.dcb.unam.mx/CoordinacionesAcademicas/CienciasAplicadas/CinematicaDinamica/sCyDecC12-2.pdf
También pueden venirte muy bien los videos sobre planos inclinados, nos cuentas ok?
Plano inclinado -
Hola me pueden ayudar con el siguiente ejercicio de velocidades relativas?
Desde tierra se observan 3 automóviles que viajan por carreteras rectas con velocidades constantes Va= 10 i m/s ; Vb= -10 j m/s ; Vc= 6 i + 8 j m/s ; Desde un sistema de referencia unido al vehículo C, Que ángulo formaran las velocidades de los vehículos A y B ?
Antonio Silvio Palmitano
el 9/11/18Tienes las expresiones de las velocidades de los móviles, expresadas en metros sobre segundo:
VA = < 10 , 0 >, VB = < 0 , -10 >, VC = < 6 , 8 >.
Luego, planteas las expresiones de las velocidades relativas de los dos primeros móviles con respecto al tercer, y queda:
VA/C = VA - VC = < 10 , 0 > - < 6 , 8 > = < 4 , -8 >, cuyo módulo es: √( (4)2+(-8)2 ) = √(80) = 4√(5);
VB/C = VA - VC = < 0 , -10 > - < 6 , 8 > = < -6 , -18 >, cuyo módulo es: √( (-6)2+(-18)2 ) = √(360) = 6√(10)-
Luego, planteas el producto escalar de las dos velocidades relativas en función de sus componentes, y queda:
VA/C•VB/C = 4*(-6) + (-8)*(-18) = -24 - 144 = -168;
luego, planteas el producto escalar de las dos velocidades relativas en función de los módulos de las mismas y del ángulo determinado por ellas, y queda:
VA/C•VB/C = 4√(5)*6√(10)*cosθ = 24*√(50)*cosθ = 24*5√(2)*cosθ = 120√(2)*cosθ;
luego, igualas las dos expresiones del producto escalar de las velocidades relativas, y queda:
120√(2)*cosθ = -168, divides en ambos miembros por 120√(2), simplificas, y queda:
cosθ = -7 / 5√(2), compones en ambos miembros con la función inversa del coseno, resuelves el segundo miembro, y queda;
θ ≅ 171,870º.
Espero haberte ayudado.
-
En un proceso de ensamblado en línea, un paquete de 20 kg parte del reposo y se desliza hacia abajo por una rampa lisa. Suponga que se quiere diseñar el dispositivo hidráulico B, mostrado en la figura, para que ejerza una fuerza constante de magnitud F sobre el paquete y lo detenga en una distancia de 100mm. ¿Cúal es la fuerza F requerida?
AYUDA
-
hola buenas tardes necesito ayuda con este problema de leyes de kepler y intensidad gravitatoria, llevo una hora intentandolo por favor si alguien me puede ayudar(es un ejercicio de 2 de bachillerato)
El periodo de revolución de la Luna alrededor de la Tierra es de 27,31 días, con un radio de
3,84·10^8 m. Calcula la intensidad de campo gravitatorio en la superficie de la Tierra.
Datos: RadioTierra 6370 km
Antonio Silvio Palmitano
el 7/11/18Tienes los datos:
ToL = 27,31 días = 27,31*24*3600 = 2359584 s (periodo orbital de la Luna),
RoL = 3,84*108 m (radio orbital de la Luna),
RT = 6370 Km = 6370*1000 = 6,370*106 m (radio de la Tierra).
Luego, puedes plantear la expresión de la velocidad angular orbital de la Luna en función de su periodo orbital, y queda:
ωoL = 2π/ToL (1).
Luego, planteas la expresión del módulo de la aceleración centrípeta orbital de la Luna en función de su velocidad angular orbital y de su radio orbital, y queda:
acp-oL = ωoL2*RoL, sustituyes la expresión señalada (1), y queda:
acp-oL = (2π/ToL)2*RoL (2).
Luego, planteas la expresión del módulo del campo gravitatorio terrestre en un punto de la órbita de la Luna (observa que es igual al módulo de la aceleración centrípeta orbital de la Luna), y queda:
G*MT/RoL = acp-oL,
sustituyes la expresión señalada (2) en el segundo miembro, y queda:
G*MT / RoL2 = (2π/ToL)2*RoL,
multiplicas por RoL2 en ambos miembros, y queda:
G*MT = (2π/ToL)2*RoL3 (3).
Luego, planteas la expresión del módulo del campo gravitatorio terrestre en un punto de la superficie de la Tierra (observa que es igual al módulo de la aceleración gravitatoria), y queda:
G*MT / RT2 = g,
multiplicas en ambos miembros por RT2, y queda:
G*MT = g*RT2 (4).
Luego, igualas las expresiones señaladas (4) (3), y queda:
g*RT2 = (2π/ToL)2*RoL3,
divides por RT2 en ambos miembros, y queda:
g = (2π/ToL)2*RoL3 / RT2,
que es la expresión del módulo de la aceleración gravitatoria terrestre en un punto de la superficie de la Tierra, en función del periodo orbital y del radio orbital de la Luna, y del radio terrestre.
Luego, solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
-
Estoy estudiando física y química en 2 de la eso y me gustaría que me resolváis y expliquéis cómo habéis hecho este problema, gracias. ¿Que altura tendría que tener un cilindro de 10 cm de radio para que se pudiese llenar con 400 g del líquido A (d=0,84 gramos partido de mililitros)? Ayúdate de la densidad del líquido A y de la fórmula del volumen del cilindro
Antonio Silvio Palmitano
el 7/11/18Tienes los datos del cilindro:
r = 10 cm (radio),
h = a determinar (altura);
por lo que la expresión de su volumen queda:
V = π*r2*h = π*102*h = 100π*h (en cm3).
Tienes los datos del líquido:
M = 400 g (masa),
δ = 0,84 g/ml = 0,84 g/cm3 (densidad, y recuerda la equivalencia entre mililitro y centímetro cúbico);
por lo que puedes plantear la expresión de su volumen, y queda:
V = M/δ = 400/0,84 (en cm3).
Luego, igualas las expresiones del volumen del cilindro que tienes remarcadas, y queda la ecuación:
100π*h = 400/0,84, divides en ambos miembros por 100π, y queda:
h = 400 / 84π ≅ 1,516 cm.
Espero haberte ayudado.
-
Hola!! La semana que viene tengo un examen de física sobre el centro de masas y cinemática 1, agradecería mucho que hicierais un video sobre esto. Llevo estudiando una semana y aun tengo dudas...
-
1. El alambre rectilíneo de longitud L [m] que muestra la figura, se encuentra uniformemente cargado con una densidad λ [C/m]. ¿Con qué rapidez v0 debe lanzarse una carga puntual q [C], desde P, ¿para que se detenga en Q? ¿Cuál debe ser el signo de q para que esto sea posible?
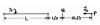 se ocupa ? ΔU=∫Fe x ds o estoy mal no logro enterder como saco la velocidad de Fuerza eléctrica
se ocupa ? ΔU=∫Fe x ds o estoy mal no logro enterder como saco la velocidad de Fuerza eléctrica Raúl RC
el 7/11/18Antonio Silvio Palmitano
el 9/11/18Te ayudo con el planteo desde el punto de vista de la energía.
Establece un sistema de referencia con eje OX sobe la recta horizontal que determinan la barra y los puntos P y Q, con sentido positivo hacia la derecha, y con origen de coordenadas en el extremo izquierdo de la barra.
Luego, elige un pequeño elemento longitudinal de carga, cuya posición puedes indicar con x, y cuya carga es: dq = λ*dx.
Luego, observa que la distancia entre el punto P y el elemento de carga es: rP = 2L-x;
y observa que la expresión del potencial en el punto P producido por el elemento de carga es:
dV = k*dq/rP = k*λ*dx/(2L-x), integras en ambos miembros (indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
VP = -k*λ*[ ln(2L-x) ], evalúas entre x = 0 y x = L (observa que son las coordenadas de los extremos de la barra cargada), y queda:
VP = -k*λ*( ln(L) - ln(2L) ) = -k*λ*ln(1/2) = k*λ*ln(2).
Luego, observa que la distancia entre el punto Q y el elemento de carga es: rQ = 4L/3-x;
y observa que la expresión del potencial en el punto Q producido por el elemento de carga es:
dV = k*dq/rQ = k*λ*dx/(4L/3-x), integras en ambos miembros (indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
VQ = -k*λ*[ ln(4L/3-x) ], evalúas entre x = 0 y x = L (recuerda que son las coordenadas de los extremos de la barra cargada), y queda:
VQ = -k*λ*( ln(L/3) - ln(4L/3) ) = -k*λ*ln(1/4) = k*λ*ln(4) = 2*k*λ*ln(2).
Luego, planteas las expresiones de la energía potencial y de la energía cinética de la carga puntual en ambos puntos, y queda:
EPP = q*VP = q*k*λ*ln(2) y ECP = (1/2)*M*vP2,
EPQ = q*VQ = 2*q*k*λ*ln(2) y ECQ = 0;
y con estos datos puedes plantear las expresiones de la energía mecánica inicial y final de la carga:
EMi = EPP + ECP = q*k*λ*ln(2) y + (1/2)*M*vP2,
EMf = EPQ + ECQ = 2*q*k*λ*ln(2) y + 0 = 2*q*k*λ*ln(2).
Luego, por conservación de la energía mecánica, puedes plantear la ecuaciòn:
EMi = EMf, sustituyes expresiones, y queda:
q*k*λ*ln(2) y + (1/2)*M*vP2 = 2*q*k*λ*ln(2), restas q*k*λ*ln(2) en ambos miembros, y queda:
(1/2)*M*vP2 = q*k*λ*ln(2), multiplicas en ambos miembros por 2/M, y queda:
vP2 = 2*q*k*λ*ln(2)/M, extraes raíz cuadrada en ambos miembros, y la expresión del módulo de la velocidad inicial de la carga queda:
vP = √(2*q*k*λ*ln(2)/M),
y observa que para que el argumento de la raíz cuadrada sea positivo, también debe serlo el valor de la carga q.
Espero haberte ayudado.
-
Hola me podrían ayudar a responder estas preguntas sobre corriente eléctrica y circuitos
>>El destello de la lampara de una cámara fotográfica es producido por la descarga de un capacitor a través de ella. ¿Por que no conectamos la lampara directamente a la fuente de alimentación con que se carga el capacitor?
>>¿Se aplican la reglas del nodo y del circuito cerrado a un circuito que contenga un capacitor?
>>¿El tiempo necesario para cargar un capacitor en un circuito RC con el fin de aumentarlo a una fracción dada de su valor final depende del valor de la fem aplicada?
Espero me ayuden.. se los agradecería

























