-
Antonio Silvio Palmitano
el 6/2/18Plantea la condición de nodo (y = 0) para la posición:
sen(5*π*x) = 0, compones en ambos miembros con la función inversa del seno, y queda:
5*π*x = k*π, con k ∈ Z;
luego, divides en ambos miembros por 5*π, y queda:
x = (1/5)*k (1).
Luego, tienes el intervalo en estudio:
0 ≤ x ≤ 0,40 (en metros);
luego, sustituyes la expresión señalada (1) en el miembro central, y queda:
0 ≤ (1/5)*k ≤ 0,40, multiplicas en los tres miembros por 5, y queda:
0 ≤ k ≤ 2, con k ∈ Z,
por lo que tienes los valores:
k = 0, que al reemplazar en la ecuación señalada (1) queda: x = 0;
k = 1, que al reemplazar en la ecuación señalada (1) queda: x = 1/5 = 0,20 m;
k = 2, que al reemplazar en la ecuación señalada (1) queda: x = 2/5 = 0,40 m.
Espero haberte ayudado.
-
Hola buenos días, me acabo de hacer pro y no se utilizar muy bien la página hay videos de física que están en YouTube y por aquí no los encuentro, por ejemplo potencial eléctrico creado por dos cargas. Alguien que me ayude! Muchas gracias!!
Dani Tallón
el 5/2/18Potencial eléctrico creado por dos cargas
¿Es este el vídeo que buscas?
Está en el desplegable de vídeos, te vas a física, 1º bachiller, en electricidad está "Campo Eléctrico y Ley de Coulomb" y el último es ese vídeo.
Espero haberte ayudado.
-
Raúl RC
el 9/2/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Hola,
Teniendo la máxima aceleración de un vehículo a, y la máxima desaceleración b, cuánto es el tiempo mínimo que tardará en recorrer una distancia d, si la velocidad inicial y final son 0.
Gracias
Antonio Silvio Palmitano
el 5/2/18Observa que debes considerar dos etapas, la primera con aceleración cuyo módulo es a, y la segunda con desaceleración cuyo módulo es b, y observa que los datos finales (posición y velocidad) de la primera etapa son los datos iniciales para la segunda.
a)
Primera etapa:
comienza por establecer un sistema de referencia con instante inicial ti = 0, con eje OX con dirección y sentido acordes con el movimiento del vehículo, con origen de coordenadas en el punto de partida de esta etapa (observa que el valor de la posición final corresponde a la distancia recorrida en esta etapa).
Tienes los datos iniciales: ti = 0, xi = 0, vi = 0, aceleración = a, taf = a determinar, xaf = a determinar, vaf = a determinar;
luego, planteas las ecuaciones de Movimiento Rectilíneo Uniformemente Acelerado, cancelas términos nulos, y queda:
xaf = (1/2)*a*taf2 (1),
vaf = a*taf (2).
b)
Segunda etapa:
comienza por establecer un sistema de referencia con instante inicial ti = 0, con eje OX con dirección y sentido acordes con el movimiento del vehículo, con origen de coordenadas en el punto de partida de esta etapa (observa que el valor de la posición final corresponde a la distancia recorrida en esta etapa).
Tienes los datos iniciales: ti = 0, xi = 0, vi = vaf, aceleración = -b, tbf = a determinar, xbf = a determinar, vbf = 0;
luego, planteas las ecuaciones de Movimiento Rectilíneo Uniformemente Acelerado, cancelas términos nulos, y queda:
xb = vaf*tbf - (1/2)*b*tbf2 (3),
0 = vaf - b*tbf (4).
Luego, tienes las relaciones entre las distancias recorridas en las etapas y los tiempos empleados en las mismas:
xaf + xbf = d (5),
t = taf + tbf (6).
Luego, sustituyes las expresiones señaladas (1) (2) en las demás ecuaciones, y queda:
xb = a*taf*tbf - (1/2)*b*tbf2 (3*),
0 = a*taf - b*tbf (4*),
(1/2)*a*taf2 + xb = d (5*),
t = taf + tbf (6).
Luego, sustituyes la expresión señalada (3*) en la ecuación señalada (5*), y queda:
0 = a*taf - b*tbf (4*), de aquí despejas: tbf = a*taf/b (4**)
(1/2)*a*taf2 + a*taf*tbf - (1/2)*b*tbf2 = d (5*),
t = taf + tbf (6).
Luego, sustituyes la expresión señalada (4**) en las ecuaciones señaladas (5*) (6), y queda:
(1/2)*a*taf2 + a2*taf2/b - (1/2)*a2*taf2/b = d (5**),
t = taf + a*taf/b, aquí extraes factor común, y queda: t = (1 + a/b)*taf (6*).
Luego, reduces términos semejantes en la ecuación señalada (5**), y queda:
(1/2)*a*taf2 + (1/2)*a2*taf2/b = d, aquí multiplicas en todos los términos de la ecuación por 2*b, y queda:
a*b*taf2 + a2*taf2 = 2*b*d, extraes factor común en el primer miembro, y queda:
taf2*(a*b + a2) = 2*b*d, haces pasajes de factores como divisores, y queda:
taf2 = 2*b*d/(a*b + a2), haces pasaje de potencia como raíz, y queda:
taf = √( 2*b*d/(a*b + a2) ) (5***);
luego, sustituyes la expresión señalada (5***) en la ecuación señalada (6*), y queda:
t = (1 + a/b)*√( 2*b*d/(a*b + a2) ).
Espero haberte ayudado.
-
Por favor ayudeme con este ejercicio, Un proyectil es disparado con un angulo de 30º por encima de la horizontal y recorre una doistancia horizontal en H antes de regresar al suelo. Si el angulo fuera de 60º y el proyectil se lanza ccon la misma rapidez ¿ que distancia horizontal recorrera ahora? desprecie la resistencia del aire
jorge velazquez
el 4/2/18como los ángulos son complementarios el alcance horizontal del proyectil con las condiciones dadas es igual
pues para un tiro parabólico perfecto tienes x=( vo2sen(2a))/g , luego nota que para el primero x1=(vo2sen(2*30))/g=(√3vo2/2g)
X2=(vo2sen(2*60))/g=(√3vo2/2g)
LUEGO SEN120=SEN60
EN CONCLUSIÓN X1=X2
NOTA: LO QUE CAMBIA ES LA ALTURA MÁXIMA ES DECIR QUE Y2>Y1 POR CAUSA DE LA COMPONENTE DE LA VELOCIDAD INICIAL EN Y ASI Vo1y=Vocos30 y Vo2y=vocos60 luego vo1y>vo2y es decir, vocos30>vocos60 asi cos30>cos60 lo que es lo mismo √3/2>1/2
-
Raúl RC
el 10/2/18Te recomiendo este video:
https://www.youtube.com/watch?v=GHL1gjBPQPo
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) envies dudas concretas, muy concretas. Y que nos envies también todo aquello que hayas conseguido hacer por ti mismo. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber cuál es tu nivel, en que podemos ayudarte, cuales son tus fallos.... Recuerda que el trabajo duro ha de ser tuyo. Nos cuentas ¿ok?
-
Hola, como se resolvería el siguiente ejercicio mediante el uso de integrales:
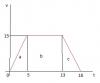
Un tren parte del reposo con una aceleración de 3 m/s2 que mantiene durante 5 segundos, al cabo de , los cuales se mantien con una velocidad constante durante 8 segundos. Finalmente, comienza a frenar, tardando 3 segundos en detenerse. Realiza la gráfica velocidad-tiempo y calcula la distancia recorrida.
Antonio Silvio Palmitano
el 4/2/18Empleamos el sistema internacional de unidades de medida, por lo que en el gráfico el tiempo se expresa en segundos y la velocidad en metros sobre segundo.
Luego, recuerda que el módulo del desplazamiento se corresponde con el área de la región determinada por el eje Ot y la gráfica de la función velocidad (observa que es la unión de dos triángulos y un rectángulo), por lo que tienes:
d = Aa + Ab + Ac = 5*15/2 + 8*15 + 3*15/2 = 75/2 + 120 + 45/2 = 180 m.
Luego, en forma analítica, puedes plantear la ecuación tiempo-posición y la ecuación tiempo-velocidad, para cada etapa (observa que reemplazamos datos e incógnitas):
a)
Movimiento Rectilíneo Uniformemente Acelerado,
ti = 0, xi = 0, vi = 0, a = 3 m/s2, tf = 5 s, xf = a determinar, vf = a determinar:
xf = 0 + 0*(5-0) + (1/2)*3*(5-0)2 = 75/2 m,
vf = 3*5 = 15 m/s.
b)
Movimiento Rectilíneo Uniforme,
ti = 5 s, xi = 75/2 m, v = 15 m/s (constante), tf = 13 s, xf = a determinar:
xf = 75/2 + 15*(13-5) = 315/2 m,
v = 15 m/s (constante).
c)
Movimiento Rectilíneo Uniformemente Desacelerado,
ti = 13 s, xi = 315/2 m, vi = 15 m/s, a = a determinar, tf = 16 s, xf = a determinar, vf = 0:
xf = 315/2 + 15*(16-13) + (1/2)*a*(16-13)2,
0 = 15 + a*(16-13);
luego, resuelves coeficientes, reduces términos numéricos, y queda:
xf = 405/2 + (9/2)*a,
0 = 15 + 3*a, aquí haces pasaje de término, y luego de factor como divisor, y queda: a = -5 m/s2;
luego, reemplazas en la primera ecuación, resuelves, y queda:
xf = 180 m.
Espero haberte ayudado.
-
Hola buenas . Siempre tengo problemas con este tipo de preguntas y nunca termino de encontrar la relación en estos ejercicios aún que los entienda. En este caso es de prensa hidráulica .
Si con una prensa hidráulica queremos multiplicar la fuerza por 16 ¿ Que relación deben cumplir sus radios?
Gracias.
Antonio Silvio Palmitano
el 3/2/18Puedes llamar F a la fuerza aplicada, y S1 = πR12 al área de la superficie sobre la cuál está aplicada.
Puedes llamar Q a la carga a equilibrar, y S2 = πR12 al área de la superficie sobre la cuál está aplicada.
Luego, plantea la condición de equilibrio (las presiones son iguales para ambas superficies):
p1 = p2, sustituyes las expresiones de las presiones, y queda:
F/S1 = Q/S2;
luego, aplicas la relación entre las fuerzas que tienes en tu enunciado (F = 16Q), sustituyes, y queda:
16Q/S1 = Q/S2;
luego, divides por Q en ambos miembros de la ecuación, y queda:
16/S1 = 1/S2; haces pasaje de divisor como factor, y queda:
16 = S1/S2; sustituyes las expresiones de las áreas de las superficies, y queda:
16 = πR12/πR22; simplificas y asocias potencias en el segundo miembro, y queda:
16 = (R1/R2)2, haces pasaje de potencia como raíz, y queda:
4 = R1/R2,
que es la relación entre los radios de las superficies.
Espero haberte ayudado.