-

Por favor me podrian colaborar con la respuesta del ejercicio 3.4, con los datos de la circunferencia. muchas graciasAntonio Silvio Palmitano
el 12/4/17Recuerda la relación entre los módulos de la aceleración centrípeta y la velocidad tangencial:
aN = v2/r, de aquí puedes despejar:
r*aN = v2, remplazas valores y queda:
0,25*7,79 = 0,0321= v2, haces pasaje de potencia como raíz y queda:
0,1791 m/s = v.
Espero haberte ayudado.
-
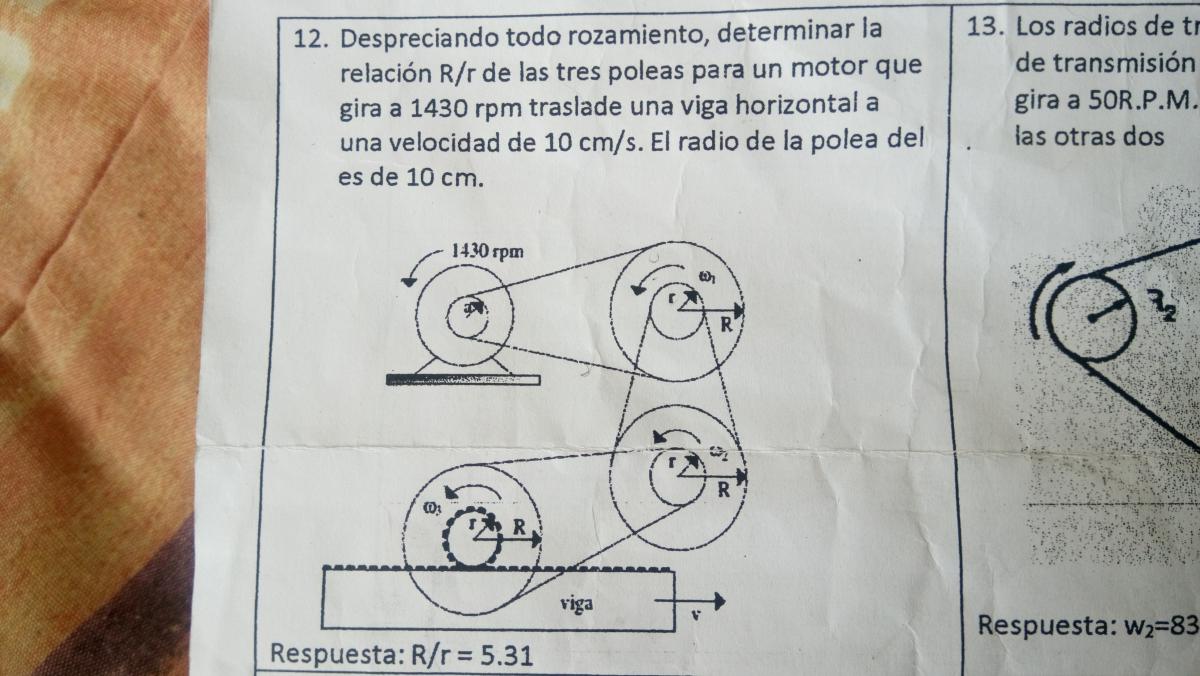
hola alguien puede ayudarme con este ejercicio?
Antonio Silvio Palmitano
el 12/4/17Observa que tienes que el radio de la polea menor del motor es r1 = 10 cm,
y que la frecuencia de giro del motor es: f1 = 1430 rev/min = 1430 rev / 60 s = (143/6) rev/s.
Observa que tenemos que la velocidad tangencial en la última polea es v4 = 10 cm/s
Luego, llamamos:
1 al sistema del motor, 2 al sistema que le sigue, 3 al siguiente y 4 al último sistema.
Luego, observa que para sistemas que comparten correa se transmite la velocidad tangencial,
y observa que dentro de cada sistema las poleas comparten eje de rotación,
por lo que se transmite la velocidad angular y la frecuencia de giro.
Luego planteamos las relaciones de transmisión.
Entre 1 y 2:
v1 = v2, expresamos las velocidades tangenciales en función de los radios y las frecuencias:
2πf1*r1 = 2πf2*R, hacemos pasajes de factor como divisor y queda:
f1*r1 = f2*R, reemplazamos valores y queda:
(143/6)*10 = f2*R, resolvemos el primer miembro y queda:
(715/3) = f2*R (A).
Entre 2 y 3 (observa que es un planteo análogo al anterior):
f2*r = f3*R (B).
Entre 3 y 4 (observa que es un planteo análogo a los anteriores):
f3*r = f4*R (C).
Luego, planteamos la relación entre velocidad tangencial, radio y frecuencia en
el sistema 4:
v4 = 2πf4*r, reemplazamos el valor de la velocidad tangencial y queda:
10 = 2πf4*r, hacemos pasajes de factores como divisores y queda:
5/π = f4*r, (D).
Luego, con ls ecuaciones señaladas A, B, C y D, tenemos el sistema:
(715/3) = f2*R
f2*r = f3*R
f3*r = f4*R
5/π = f4*r, de aquí despejamos: (5/π)*(1/r) = f4 (E)
multiplicamos miembro a miembro con las tres primeras ecuaciones y queda:
(715/3)*f2*r*f3*r = f2*R*f3*R*f4*R, hacemos pasajes de factores, y queda:
(715/3)*r2 = R3*f4 sustituimos la expresión señalada (E) y queda:
(715/3)*r2 = R3*(5/π)*(1/r), hacemos pasajes de factores como divisores y queda:
(715/3) / (5/π) = R3/r3, resolvemos el primer miembro y queda:
149,7492 = R3/r3, asociamos potencias y queda:
149,7492 = (R/r)3, hacemos pasaje de potencia como raíz y queda:
5,3103 = R/r.
Espero haberte ayudado.
-
Podrías hacer un vídeo en el que expliques los MRUR (Movimiento Uniforme Rectilíneo Retardado), es que he estado mirando tus vídeos y no he encontrado nada parecido que me ayude con mis dudas.
Muchas gracias :)
-
¡Hola! En un ejercicio me puden calcular a qué distancia horizontal caerá un objeto. Sabiendo que cae de un avión en movimiento, ¿Tengo que calcular caída libre en lugar de parabólica? Me descuadra que especifique que la distancia a calcular sea horizontal. ¡Gracias!
Raúl RC
el 12/4/17Este ejercicio trata sobre tiro horizontal y no parabólico, te recomiendas veas este vídeo:
https://www.youtube.com/watch?v=t1WF0w38lYE
Nos cuentas ;)
-
Buenas tenía una duda únicamente con el apartado c, lo he planteado como el resto suponiendo que el sumatorio de fuerzas en el eje x es 0, por tanto me queda que la fuerza debe de ser igual al rozamiento de b con el suelo + el rozamiento que ejerce a sobre b + la tensión, pero no sé como calcular la tensión de la cuerda. Un saludo y gracias.
Raúl RC
el 12/4/17Hola! Nos encantaría ayudarte, pero no respondemos dudas que se salgan del contenido general de secundaria y bachiller.
No obstante seria de agradecer que nos enviaras paso a paso todo lo que has hecho, para que viéramos dónde te lias y a partir de ahi poder orientarte.
Un saludo.
Antonio Silvio Palmitano
el 12/4/17c) Establecemos dos direcciones: OX paralela al suelo, con sentido positivo hacia la derecha, y OY perpendicular al suelo, con sentido positivo hacia arriba. Consideramos que la polea y la soga son ideales.
Luego, observa que las fuerzas que actúan sobre el bloque A son:
Acción Normal del bloque B sobre él, vertical hacia arriba,
Peso, vertical hacia abajo,
Tensión de la soga: horizontal hacia la izquierda,
Rozamiento del bloque B sobre él, horizontal hacia la derecha;
luego, plantea la condición de equilibrio para cada dirección, más la expresión del módulo de la fuerza de rozamiento (expresamos al módulo del peso como producto de masa por aceleración gravitatoria):
frAB - T = 0
NAB - MAg = 0
frAB = μNAB
Luego, observa que las fuerzas que actúan sobre el bloque B son:
Reacción Normal del bloque A sobre él, vertical hacia abajo,
Peso, vertical hacia abajo,
Acción Normal del suelo sobre él, vertical hacia arriba,
Tensión de la soga: horizontal hacia la izquierda,
Reacción al rozamiento del bloque A sobre él, horizontal hacia la izquierda,
Rozamiento del suelo sobre él, horizontal hacia la izquierda,
Fuerza realizada sobre él por un agente externo, horizontal hacia la derecha;
luego, plantea la condición de equilibrio para cada dirección, más la expresión del módulo de la fuerza de rozamiento:
F - frAB - T - frB = 0
NB - NAB - MBg = 0
frB = μNB
Luego con las seis ecuaciones que tienes planteadas, tienes un sistema con seis incógnitas:
frAB, T, NAB, F, frB, NB.
Luego, reemplazas valores (empleamos el Sistema Internacional de Unidades de Medida) y queda:
frAB - T = 0,
NAB - 49 = 0, de aquí tienes: NAB = 49 N
frAB = 0,2*NAB
F - frAB - T - frB = 0
NB - NAB - 147 = 0
frB = 0,2*NB
sustituyes las expresiones de los módulos de las fuerzas de rozamiento, reemplazas el valor remarcado y queda:
9,8 - T = 0, de aquí tienes: 9,8 N =T
F - 9,8 - T - frB = 0
NB - 196 = 0, de aquí tienes: NB = 196 N
frB = 0,2*NB
reemplazas el valor remarcado y queda:
F - 9,8 - 9,8 - frB = 0
frB = 0,2*196
resuelves y ordenas términos, y queda:
F - frB = 19,6
frB = 39,2 N
reemplazas en la primera ecuación y queda:
F - 39,2 = 19,6
F = 58,8 N.
Espero haberte ayudado.
-
Buenas noches, espero que se encuentren bien, vengo a pedirles un poco de ayuda en fisica ya que me encuentro viendo movimiento unidimensional con aceleracion constante y no logro entender muy bien como resolver este tipo de ejercicios, a continuacion les adjuntare a una imagen de un problema que me ha causado problemas valga la redundancia, espero que puedan ayudarme u orientarme de alguna manera! Muchisimas gracias!

Raúl RC
el 12/4/17Antonio Silvio Palmitano
el 12/4/17Observa que ambos móviles se desplazan primero con Movimiento Rectilíneo Uniformemente Acelerado, y luego con Movimiento Rectilíneo Uniforme, y observa que la posición final y la velocidad final de su primera etapa son la posición inicial y la velocidad inicial de su segunda etapa.
Consideramos un eje de posiciones OX con origen en el punto de partida, y sentido positivo coincidente con el sentido de movimiento de los móviles.
Luego, para la primera etapa del patinador tenemos: t0 = 0, x0 = 0, v0 = 0, a = 4,5 m/s2,
su ecuación de movimiento es: x = (1/2)*4,5*t2 = 2,25*t2, y su posición final es:
x = 2,25*32 = 20,25 m;
y su ecuación de velocidad es: v = 4,5*t, y su velocidad final es:
v = 4,5*3 = 13,5 m/s.
Luego, para su segunda etapa tenemos: t0 = 3 s, v = 13,5 m/s (constante),
su ecuación de movimiento es:
x = 20,25 + 13,5*(t - 3),
y su ecuación de velocidad es:
v = 13,5.
Finalmente, la expresión de la función de posición para el patinador queda:
xp =
2,25*t2 para 0 ≤ t ≤ 3
20,25 + 13,5*(t - 3) para t > 3
Luego, para la primera etapa del ciclista tenemos: t0 = 1,5 s, x0 = 0, v0 = 0, a = 2,75 m/s2,
su ecuación de movimiento es: x = (1/2)*2,75*(t - 1,5)2 = 1,375*(t - 1,5)2, y su posición final es (t = 1,5 + 6,25 = 7,75 s):
x = 1,375*(7,75 - 1,5)2 = 53,7109375 m;
y su ecuación de velocidad es: v = 2,75,5*(t - 1,5), y su velocidad final es:
v = 2,75*(7,75 - 1,5) = 17,1875 m/s.
Luego, para su segunda etapa tenemos: t0 = 7,75 s, v = 17,1875 m/s (constante),
su ecuación de movimiento es:
x = 53,7109375 + 17,1875*(t - 7,75),
y su ecuación de velocidad es:
v = 17,1875.
Finalmente, la expresión de la función de posición para el patinador queda:
xc =
1,375*(t - 1,5)2 para 1,5 ≤ t ≤ 7,75
53,7109375 + 17,1875*(t - 7,75) para t > 7,75
Luego, evaluamos posiciones en los instantes notables, y los consignamos en una tabla:
t xp xc
0 0 0 instante de partida del patinador
1,5 5,0625 0 instante de partida del ciclista el patinador va adelante
3 20,25 3,09375 el patinador cambia su movimiento el patinador va adelante
7,75 84,375 53,7109375 el ciclista cambia su movimiento el patinador va adelante
Luego, observa que el instante de encuentro se produce cuando ambos móviles se desplazan con Movimiento Rectilíneo Uniforme, por que planteamos la condición de encuentro:
xp = xc, reemplazamos expresiones y queda:
20,25 + 13,5*(t - 3) = 53,7109375 + 17,1875*(t - 7,75), distribuimos agrupamientos y queda:
20,25 + 13,5*t - 40,5 = 53,7109375 + 17,1875*t - 133,203125, hacemos pasajes de términos y queda:
- 3,6875*t = - 59,2421875, hacemos pasaje de factor como divisor y queda:
t ≅ 16,0657 s.
Luego, reemplazamos en la función de posición del patinador y queda:
xp ≅ 20,25 + 13,5*(16,0657 - 3) = 196,6367 m;
y puedes verificar la validez de la solución si reemplazas en la ecuación del ciclista.
Espero haberte ayudado.
-
Raúl RC
el 12/4/17Hola Jose...espero este vídeo te sirva.
https://www.youtube.com/watch?v=LEcvpSzbYKA
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok?
-
Tengo este problema y no he encontrado ninguna solución por ahí:
Un automóvil que pesa 1000 Kg desciende por una cuesta de 10º de inclinación. El conductor divisa un obstáculo y aplica los frenos produciendo una fuerza total de frenado (aplicada por la carretera sobre los neumáticos) constante y de 5000 N. Hasta que el coche se detiene recorre una distancia de 200 m.
El problema pide averiguar la velocidad inicial del vehículo
gemelo
el 12/4/17Antonio Silvio Palmitano
el 14/4/17Vamos con un planteo a partir de consideraciones de energía y trabajo.
Puedes plantear, a partir de un sistema de coordenadas con eje OX paralelo al piso y con eje OY perpendicular y que contiene al punto en el cuál el conductor del auto aplica los frenos, que las posiciones y velocidades son (observa que llamamos L a la longitud de la rampa inclinada, que es igual a 200 m):
al Inicio: x0 = 0, y0 = L*sen(10°), v0 = a determinar,
luego su energía mecánica inicial queda:
EM0 = EP0 + EC0 = M*g*y0 + (1/2)*M*v02;
al final: x = L*cos(10°), y = 0, v = 0 (se detiene el auto);
luego su energía mecánica final queda:
EM = EP + EC = M*g*y + (1/2)*M*v2 = M*g*0 + (1/2)*M*02 = 0.
Luego planteamos el trabajo de la fuerza de frenado (cuyo módulo es 5000 N), y observa que es paralela a la dirección de movimiento, pero con sentido contrario):
Wfr = - fr*L.
Luego, planteamos que el trabajo de la fuerza de frenado es igual a la variación de energía mecánica del auto:
Wfr = - EM - EM0, sustituimos y queda:
- fr*L = 0 - M*g*y0 + (1/2)*M*v02, cancelamos el término nulo, hacemos pasaje de término y queda:
M*g*y0 - fr*L = (1/2)*M*v02, multiplicamos en todos los términos de la ecuación por 2/M y queda:
2*g*y0 - 2*fr*L/M = v02, haces pasaje de potencia como raíz y tienes:
√(2*g*y0 - 2*fr*L/M) = v0, que es el módulo de la velocidad inicial del auto, que corresponde al momento en que el conductor aplica los frenos.
Solo queda que realices el cálculo.
Espero haberte ayudado.
-
Hola que tal tengo una pregunta sobre dinamica. Tengo que responder verdadero o falso y justificar.
Un cuerpo sobre el que actúan varias fuerzas, puede moverse con velocidad constante.



























