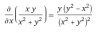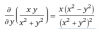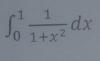-
Fernando Quispe Reynolds
el 1/7/18 -
Izabela iosub
el 1/7/18 -
Jose
el 1/7/18 -
Mario
el 1/7/18 -
Froylan
el 1/7/18 -
Nacho
el 1/7/18Hola Unicoos, estoy resolviendo este problema y como no indica la opcion correcta me gustaria saber si la respuesta correcta es la opcion C:
Nacho
el 1/7/18 -
Imanol Carreras
el 1/7/18
Holaa, como se hace este?
Antonio Silvio Palmitano
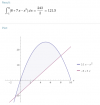
el 1/7/18Comienza por determinar los puntos de intersección entre las gráficas de las dos funciones, para ello igualas expresiones, y queda la ecuación:
x2 + 3 = 2x + 6, restas 2x y restas 6 en ambos miembros de la ecuación, y queda:
x2 - 2x - 3 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
x1 = -1 y x2 = 3.
Luego, planteas la integral cuyo argumento es la resta entre las dos expresiones de las funciones, y tienes:
I = -1∫3 ( (x2 + 3) - (2x + 6) )*dx = distribuyes agrupamientos, reduces términos semejantes, y queda:
= -1∫3 ( (x2 - 2x - 3)*dx = integras (indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
= [ x3/3 - x2 - 3x ] = evalúas, y queda:
= (9 - 9 - 9) - (-1/3 - 1 + 3) = resuelves agrupamientos, y queda:
= -9 - 5/3 = -32/3.
Luego, como la integral es negativa, tienes que su valor es el opuesto al valor del área comprendida entre las dos gráficas de las funciones y sus dos puntos de intersección, por lo que puedes plantear:
A = -I = -(-32/3) = 32/3.
Espero haberte ayudado.
-
Froylan
el 1/7/18Hola me pueden ayudar con está integral definida, no se como se resuelva, ayuda por favor
}
Antonio Silvio Palmitano
el 1/7/18Debes observar que es una integral con resolución directa (indicamos con corchetes que debes evaluar con Regla de Barrow):
I = [ arctanx ] = arctan(1) - arctan(0) = π/4 - 0 = π/4.
Observa que si tienes la función cuya expresión es:
f(x) = arctanx,
entonces tienes que la expresión de su función derivada es:
f ' (x) = 1/(1+x2).
Espero haberte ayudado.
-
Juan Izarra Castaños
el 1/7/18Hola , tengo una duda en el apartado c) de esta pregunta del examen de matemáticas de junio 2018 (País Vasco). ¿Cómo sé cuales son los puntos (x, y) enteros en el espacio de soluciones del apartado a? una vez conocidos los punto sí se calcular el máximo.
Tengo la prueba extraordinaria el miércoles y te lo agradezco si me lo puedes contestar rápido.Gracias
Antonius Benedictus
el 1/7/18
Juan Izarra Castaños
el 1/7/18Entonces, tengo que evaluar todos los puntos enteros dentro del recinto (1,2) (1,3) (1,4) (1,5) (2,1) (2,2) (2,3) (3,0) (3,1)?
No ha una forma más sencilla, porque al dibujarlo en un folio puedes tener dudas de los puntos que entran o no. Por ejemplo el punto (1, 5) no sabia si quedaba dentro o fuera del recinto cuando he hecho yo la gráfica.
