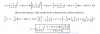-
Buenas... tengo estos 2 ejercicios que no pude resolver la d tengo idea de como hacer y debo evitar la area negativa graficar y trabajar desde 0 hasta pi/2 ya lo tengo planteado la d.... pero en la c es donde me pierdo porque al intentar despejar x no pude.... y luego al usar los valores del primer cuadrante de 0 a pi/2 ( no se si estara bien estos datos) no pude graficar ..... en si el ejercicio C no puedo resolverlo quisiera que alguien me ayude por favor de antemano gracias
-
Hola, podrían orientarme con el siguiente ejercicio. No se exactamente lo que tengo que hacer.
Si x =a+2b -3c, y = b+ 2c - 3a, z =c + 2a -3b, prueba que x + y + z = 0.
Facundo Soria
el 30/6/18una forma de hacer ese ejercicio es reemplazar donde te dicen x + y+ z =0 poner (a+2b-3c) + (b+2c-3a) + (c+2a-3b) = 0 (esto es debido a que x es a+2b-3c, (y) es b+2c-3a y (z) es c+2a-3b)
(a+2b-3c) + (b+2c-3a) + (c+2a-3b) = 0
(a-3a+2a) + (2b+b-3b) + (c+2c-3c) = 0
0 a + 0 b + 0 c = 0
0 = 0
por lo tanto se verifica que x + y + z = 0
espero haberte ayudado.
-
Hola unicoos... Podrian ayudarme para resolver esta igualdad..... La incognita es costos fijo (CF)...
UaII=Utilidad antes de impuesto...P=precio.....Q=Cantida....Cv=costo variable..... CF=costo fijo....EL CF TIENE QUE DAR 21.000
Reemplazando los datos queda:
UaII=P*Q-Cv-CF
26.250=120*946-70,05-CF
Antonius Benedictus
el 2/7/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Antonio Silvio Palmitano
el 29/6/18Tienes la expresión de una función racional (observa que es un cociente entre dos polinomios), cuyo denominador se anula en x = -2 y en x = 2 (recuerda que estos valores los obtienes a partir de resolver la ecuación que queda al igualar el denominador a cero), por lo que el dominio de la función queda:
D = (-∞,-2) u (-2,2) u (2,+∞) = { x ∈ R : x ≠ -2 y x ≠ 2 },
por lo que tienes que la gráfica de la función presenta dos puntos de discontinuidad, cuyas abscisas son:
x1 = -2 y x2 = 2, que debes considerar por separado, por medio de la definición de continuidad de una función en un valor de su dominio.
1°)
Para x1 = -2 tienes:
a)
la función no está definida en este valor del dominio;
b)
Lím(x→-2-) f(x) = Lím(x→-2-) (x2-5x+6)/(x2-4) = +∞,
ya que el numerador tiende a 20 y el denominador tiende a cero desde valores positivos,
Lím(x→-2+) f(x) = Lím(x→-2+) (x2-5x+6)/(x2-4) = -∞,
ya que el numerador tiende a 20 y el denominador tiende a cero desde valores negaitivos;
c)
observa que la gráfica de la función presenta una asíntota vertical cuya ecuación es: x = -2.
2°)
Para x2 = 2 tienes:
a)
la función no está definida en este valor del dominio;
b)
Lím(x→2) f(x) = Lím(x→2) (x2-5x+6)/(x2-4) = factorizas:
= Lím(x→2) (x-2)(x-3) / (x+2)(x-2) = simplificas:
= Lím(x→2) (x-3) / (x+2) = -1/4
ya que el numerador tiende a -1 y el denominador tiende a 4;
c)
observa que la gráfica de la función presenta una discontinuidad puntual (o evitable) para este valor del dominio de la función.
Espero haberte ayudado.
-
Buenas tardes, quisiera saber si me pueden ayudar a resolver la siguiente proposición, porque no sé cómo demostrar su valor de verdad! Muchas gracias

Antonio Silvio Palmitano
el 29/6/18Consideramos al conjunto de los números naturales con primer elemento igual a cero:
N = { 0 , 1 , 2 , 3 , ... }.
Luego, observa que para el primer elemento (y = 0) tienes la inecuación:
x + 1 ≤ 0, aquí restas uno en ambos miembros, y queda:
x ≤ -1, y como -1 pertenece al conjunto de los números enteros, tienes que él (o cualquier otro número entero menor que él) verifican que la proposición es Verdadera (en palabras sencillas: "un número entero negativo es menor o igual que cualquier número natural").
Luego, tienes la proposición:
P(x,y): ∃x∈Z / ( ∀y∈N, x+1≤y ),
planteas la negación trivial, y queda:
∼P(x,y): ∼[ ∃x∈Z / ( ∀y∈N, x+1≤y ) ],
planteas la negación con el primer cuantificador (recuerda que debes cambiar el cuantificador y negar el predicado), y queda:
∼P(x,y): ∀x∈Z / ∼( ∀y∈N, x+1≤y ),
planteas la negación con el segundo cuantificador (recuerda que debes cambiar el cuantificador y negar el predicado), y queda:
∼P(x,y): ∀x∈Z / [ ∃y∈N, ∼(x+1≤y) ],
expresas al predicaco en una forma afirmativa equivalente, y queda:
∼P(x,y): ∀x∈Z / [ ∃y∈N, x+1>y ].
Espero haberte ayudado.
-
Hola como puedo factorizar este polinomio 2x4 - 5x2 -3= 0 Se que se puede factorizar como (x2 -3) (2x2 +1)= 0 Pero no se como llegar a esa factorización He intentado división sintetica o riffini pero no sirve.
De antemano gracias.
Antonio Silvio Palmitano
el 29/6/18Tienes la expresión del polinomio:
P(x) = 2x4 - 5x2 - 3;
luego, planteas la sustitución (camio de variable):
x2 = w (1) (observa que w toma valores positivos), de donde tienes:
x4 = (x2)2 = w2;
luego, sustituyes en la expresión del polinomio, y queda:
P(w) = 2w2 - 5w - 3 = 0 (2),
que es una ecuación polinómica cuadrática cuyas soluciones son:
w1 = -1/2,
w2 = 3;
luego, puedes factorizar la expresión señalada (2), y queda:
P(w) = 2(w + 1/2)(w - 3),
luego sustituyes la expresión señalada (1), y queda
P(x) = 2(x2 + 1/2)(x2 - 3),
que es una forma del polinomio, parcialmente factorizada en el campo de los números reales;
luego, factorizas el último agrupamiento (observa que tienes una diferencia de cuadrados), y queda:
P(x) = 2(x2 + 1/2)( x - √(3) )( x + √(3) ),
que es la expresión factorizada del polinomio en el campo de los números reales, ya que el polinomio del primer agrupamiento no tiene raíces reales).
Espero haberte ayudado.
-
Antonio Silvio Palmitano
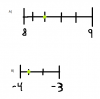
el 29/6/18A)
Observa que tienes un segmento cuya longitud es: L = 9-8 = 1, que está dividido en cinco partes iguales, por lo que cada una de esas partes tiene longitud igual a: L/5 = 1/5.
Luego, como el extremo izquierdo del segmento es 8, tienes para el punto remarcado (observa que se encuentra a la derecha del extremo izquierdo, y que los valores crecen) en tu imagen:
x = 8 + 1/5 = 8*5/5 + 1/5 = 40/5 + 1/5 = (40+1)/5 = 41/5,
que es una expresión equivalente a la solución que indica el colega Rober.
B)
Observa que tienes un segmento cuya longitud es: L = -3-(-4) = -3+4 = 1, que está dividido en tres partes iguales, por lo que cada una de esas partes tiene longitud igual a: L/3 = 1/3.
Luego, como el extremo izquierdo del segmento es -4, tienes para el punto remarcado (observa que se encuentra a la derecha del extremo izquierdo, y que los valores crecen) en tu imagen:
x = -4 + 1/3 = -4*3/3 + 1/3 = -12/3 + 1/3 = (-12+1))/3 = -11/3,
que es la expresión de la solución que indica el colega Rober.
Espero haberte ayudado.