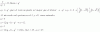-
Hola tengo una duda con este enunciado como se harian estos ejercicios:
PD: SON EJERCICIOS DE REPASO PERO NO LOS SÉ HACER SI PUDIERAN AYUDARME.GRACIAS Y BUENOS DÍAS. -
Hola., me pueden ayudar con estos ejercicios..? todos o los que puedan...

Marcos
el 20/6/18 -
Hola Unicoos, por fis me podrian ayudar con este ejercicio es por Jacobi y Seidel

David
el 21/6/18Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Hola Buenas Noches o Buenos Días, Mi duda es Sobre Integrales Impropias
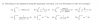
Por ejemplo el ejercicio (a) me encuentro con el problema de cuando hago tender una variable t a Infinito de la integral de 1 hasta t
me queda una integral que al resolverla por partes podría estar toda una vida dándome un u,du,dv ,y se que se puede hacer por criterio de comparación, entonces alguien me podría explicar dicho criterio y como lo aplico a este caso en particular,se los agradecería un montón
César
el 20/6/18 -
Hola, podrían ayudarme con este tema por favor, muchas gracias!
Calcule la longitud del arco de curva C: r- = r-(t) = t3 i- + 3t2 j- +6t k- Desde el punto A (0,0,0) hasta B (1,3,6)
Antonio Silvio Palmitano
el 20/6/18Tienes la expresión de la función vectorial de posición de los puntos de la curva:
r(t) = < t3 , 3*t2 , 6*t >,
y observa que los valores del parámetro que corresponden a los puntos A y B son: tA = a = 0 y tB = b = 1.
Luego, planteas la expresión de la función derivada, y queda:
r ' (t) = < 3*t2 , 6*t , 6 >,
cuyo módulo elevado al cuadrado queda expredado:
|r ' (t)|2 = (3*t2)2 + (6*t)2 + (6)2, resuelves en cada término, y queda:
|r ' (t)|2 = 9*t4 + 36*t2 + 36, extraes factor común, y queda:
|r ' (t)|2 = 9*(t4 + 4*t2 + 4), factorizas el trinomio cuadrado perfecto en el agrupamiento, y queda:
|r ' (t)|2 = 9*(t2 + 2)2, extraes raíz cuadrada en ambos miembros (observa que elegimos la raíz positiva), y queda:
|r ' (t)| = 3*(t2 + 2), distribuyes, y queda:
|r ' (t)| = 3*t2 + 6,
que es la expresión del módulo de la función derivada.
Luego, puedes plantear para la longitud de la curva entre los puntos A y B:
L = a∫b |r ' (t)|*dt,
sustituyes la expresiones remarcadas, y queda:
L = 0∫1 (3*t2 + 6)*dt,
integras (observa que indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
L = [ t3 + 6*t ],
evalúas, y queda:
L = (1 + 6) - (0 + 0),
resuelves, y queda:
L = 7.
Espero haberte ayudado.
Erick
el 20/6/18 -
Antonio Silvio Palmitano
el 19/6/18Observa que tienes dos puntos del plano:
P1(3,1,-1) y P2(0,0,-3),
y con ellos puedes plantear la expresión de un vector (u) paralelo al plano buscado:
u = P1P2 = < 0-3 , 0-1 , -3-(-1) > = < -3 , -1 , -2 >.
Luego, tienes la ecuación cartesiana implícita del plano en tu enunciado, de donde tienes que la expresión del vector normal al plano π es:
nπ = < 2 , -2 , 1 >,
y como tienes que este plano es perpendicular al plano buscado, entonces tienes que su vector normal es paralelo a él.
Luego, puedes proponer que el producto vectorial entre los vectores paralelos al plano buscado es un vector normal a dicho plano, por lo que tienes:
N = u x nπ = < -3 , -1 , -2 > x < 2 , -2 , 1 > = < -5 , -1 , 8 >.
Luego, con la expresión del vector N y las coordenadas de uno de los puntos del plano (observa que elegimos el punto P1), planteas una ecuación cartesiana implícita del plano buscado, y queda:
-5*(x - 3) - 1*(y - 1) + 8*(z + 1) = 0,
distribuyes en todos los términos, reduces términos semejantes, ordenas términos, y queda:
-5*x - 1*y + 8*z + 24 = 0,
que es una ecuación cartesiana implícita del plano buscado
Espero haberte ayudado.
-
Hallar el número n= aabb sabiendo que es un cuadrado perfecto!
Antonio Silvio Palmitano
el 19/6/18Planteas la expresión del número como suma de múltiplos de potencias de 10, y queda:
n = 1000a + 100a + 10b + b, reduces términos semejantes, y queda:
n = 1100a + 11b, extraes factor común, y queda:
n = 11(100a + b) (1),
y observa que a partir de la expresión señalada (1) tienes que n es múltiplo de 11, y como es un cuadrado perfecto, tienes que su segundo factor también tiene que se múltiplo de 11, con otro factor que a su vez debe ser un cuadrado perfecto, por lo que puedes plantear:
100a + b = 11k2, con k ∈ N (2),
sustituyes la expresión señalada (2) en la ecuación señalada (1), y queda:
n = 11*11k2 = 112*k2 = (11k)2 (3).
Luego, planteas los valores para diferentes números naturales (k = 1, 2, 3, ...), y tienes:
n = 121, 484, 1089, 1936, 3025, 4356, 5929, 7744, 9801, 12100;
y observa que el valor remarcado corresponde a k = 8,
y que la expresión del número n como multiplicación de potencias con factores primos es:
n = (11*8)2= (11*23)2 = 112*26.
Espero haberte ayudado.
-
Probar que si a-b es múltiplo de 2, entonces a+b es múltiplo de 2
AYUDA!!!
XIME
el 19/6/18Antonio Silvio Palmitano
el 19/6/18Vamos con la idea que expone el colega Evaristo.
Tienes en tu enunciado que a-b es múltiplo de 2, por lo que tienes:
a - b = 2*k, con k ∈ Z,
aquí sumas b en ambos miembros, y queda:
a = 2*k + b (1).
Luego, te piden probar que el número entero: a+b es múltiplo de 2, por lo que planteas:
a + b = sustituyes la expresión señalada (1) en el primer término, y queda:
= 2*k+b + b = reduces términos semejantes, y queda:
= 2*k + 2*b = extraes factor común, y queda:
= 2*(k + b),
por lo que tienes que el número entero: a+b es el doble del número entero: k+b,
por lo que puedes concluir que el número entero: a+b es múltiplo de 2.
Espero haberte ayudado.