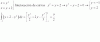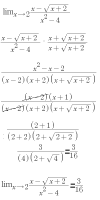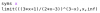-
-
Me pueden ayudar por favor. 4º ESO
1.- Para los siguientes datos ("x" indica ejercicios repasados, "y" indica la nota sacada en el examen), calcula e interpreta el coeficiente de correlación lineal:
∑ xi fi = 61, ∑ yj fj = 63, ∑ x2i fi = 409, ∑ y2j fj = 441 ∑ xi yj fij =422, N = 10
Muchas gracias.
-
 Sean los vectores u1 = (1, 1, 0); u2 = (0, 1,
1); u3 = (1, 0, 1)
2 R3, y v1 = (1, 1,
0, 0); v2 =
(0, 1, 2, 1);
v3 = (1,
1,
4,
2)
2 R4 y f : R3 --> R4 la aplicacion lineal definida por f(ui) = vi
para cualquier i = 1, 2, 3.
Sean los vectores u1 = (1, 1, 0); u2 = (0, 1,
1); u3 = (1, 0, 1)
2 R3, y v1 = (1, 1,
0, 0); v2 =
(0, 1, 2, 1);
v3 = (1,
1,
4,
2)
2 R4 y f : R3 --> R4 la aplicacion lineal definida por f(ui) = vi
para cualquier i = 1, 2, 3.
a) Calcula la matriz A = M(f)B0 B , donde B y B0 son las bases canonicas de R3 y R4 respectivamente.
b) Calcula el nucleo y la imagen de la aplicacion y di si la aplicacion es inyectiva o sobreyectiva.
está bien hecho?
Antonio Silvio Palmitano
el 19/6/18Vamos con una orientación.
Expresas a los vectores u1, u2 y u3 como combinaciones lineales de los vectores canónicos, y quedan:
u1 = <1,0,0> + <0,1,0>,
u2 = <0,1,0> + <0,0,1>,
u3 = <1,0,0> + <0,0,1>.
Luego, planteas las expresiones de sus transformados (observa que tienes un aplicación lineal, por lo que puedes transformar término a término, y quedan las ecuaciones vectoriales:
f(1,0,0) + f(0,1,0) = <1,1,0,0>, de aquí despejas: f(1,0,0) = <1,1,0,0> - f(0,1,0) (1),
f(0,1,0) + f(0,0,1) = <0,1,2,1>, de aquí despejas: f(0,0,1) = <0,1,2,1> - f(0,1,0) (2),
f(1,0,0) + f(0,0,1) = <1,1,4,2> (3);
luego, sustituyes las expresiones señaladas (1) (2) en la ecuación señalada (3), y queda
<1,1,0,0> - f(0,1,0) + <0,1,2,1> - f(0,1,0) = <1,1,4,2>, reduces términos semejantes, y queda:
-2*f(0,1,0) + <1,2,2,1> = <1,1,4,2>, restas <1,2,2,1> en ambos miembros, y queda:
-2*f(0,1,0) = <0,-1,2,1>, multiplicas por -1/2 en ambos miembros, y queda:
f(0,1,0) = <0,1/2,-1,-1/2>;
luego, remplazas la expresión remarcada en las ecuaciones señaladas (1) (2), y queda
f(1,0,0) = <1,1,0,0> - <0,1/2,-1,-1/2> = <1,1/2,1,1/2>,
f(0,0,1) = <0,1,2,1> - <0,1/2,-1,-1/2> = <0,1/2,3,3/2>.
a)
Con las expresiones remarcadas de los transformados de los vectores canónicos de R3, puedes plantear la expresión de la matriz asociada a la aplicación lineal:
Af =
0 1 0
1/2 1/2 1/2
-1 1 3
-1/2 1/2 3/2.
Luego, multiplicas a la matriz por un vector genérico del dominio (R3): <x,y,z> (escrito en columna), y tienes la expresión general de la aplicación lineal:
f(x,y,z) = < y , x/2+y/2+z/2 , -x+y+3z , -x/2+y/2+3z/2 > (*).
b1)
Planteas la condición que cumple un elemento genérico del núcleo de la aplicación, y queda:
f(x,y,z) = <0,0,0,0>, sustituyes la expresión del vector transformado, y queda:
< y , x/2+y/2+z/2 , -x+y+3z , -x/2+y/2+3z/2 > = < 0 , 0 , 0 , 0 >,
igualas componente a componente, y queda el sistema de ecuaciones:
y = 0,
x/2+y/2+z/2 = 0,
-x+y+3z = 0,
-x/2+y/2+3z/2 = 0;
luego, multiplicas por 2 en todos los términos de la segunda y de la cuarta ecuación, cancelas términos nulos en las últimas tres ecuaciones , multiplicas por 2 en todos los términos de la segunda y de la cuarta ecuación, y queda:
x + z = 0,
-x + 3z = 0,
-x + 3z = 0,
resuelves el sistema (observa que las dos últimas ecuaciones son coincidentes), y queda: x = 0, z = 0;
por lo que tienes que el único elemento que pertenece al núcleo de la transformación es el vector nulo, por lo que el núcleo de la aplicación queda expresado:
Nf = { <0,0,0> }, y su dimensión es cero.
b2)
Observa que la expresión señalada (*) es la expresión de un vector genérico de la imagen de la aplicación (w), por lo que puedes plantear:
w = < y , x/2+y/2+z/2 , -x+y+3z , -x/2+y/2+3z/2 >,
descompones la expresión como sumas de vectores según las indeterminadas, y queda:
w = <0,x/2,-x,-x/2> + <y,y/2,y,y/2> + <0,z/2,3z,3z/2>,
extraes factores escalares, y queda:
w = (x/2)*<0,1,-2,-1> + (y/2)*<2,1,2,1> + (z/2)*<0,1,6,3>;
por lo que tienes que un conjunto generador de la imagen queda expresado:
GI = { <0,1,-2,-1> , <2,1,2,1> , <0,1,6,3> },
y puedes probar (te dejo la tarea) que los tres vectores del conjunto son linealmente independientes, por lo que tienes que el conjunto GI es una base de la imagen de la aplicación, cuya dimensión es tres.
b3)
Observa que la dimensión del codominio (R4) es cuatro, que es mayor que la dimensión de la imagen que es tres, por lo que tienes que la imagen es un subconjunto incluido en el dominio pero que no es igual a él, por lo que tienes que la aplicación no es sobreyectiva.
b4)
Como tienes que el núcleo de la aplicación tiene dimensión cero, tienes que el vector nulo del dominio es el único vector que se relaciona con el vector nulo de la imagen, por lo que tienes que la aplicación es inyectiva (recuerda que a dos vectores distintos del dominio que no pertenezcan al núcleo de la aplicación, le corresponden vectores distintos de la imagen).
Espero haberte ayudado.
-
alguein me podría ayudar a resolver estos problemas:
1)Escribí la ecuacion reducida de la elipse cuya distancia focal es 10 y cuyo semieje mayor tiene longitud 13
2)Encontrá la ecuación reducida de la elipse cuyo semieje mayor tiene longitud 5 y qye pasa por P=(4,1)
gracias
-
ayuda con estos límites por favor,
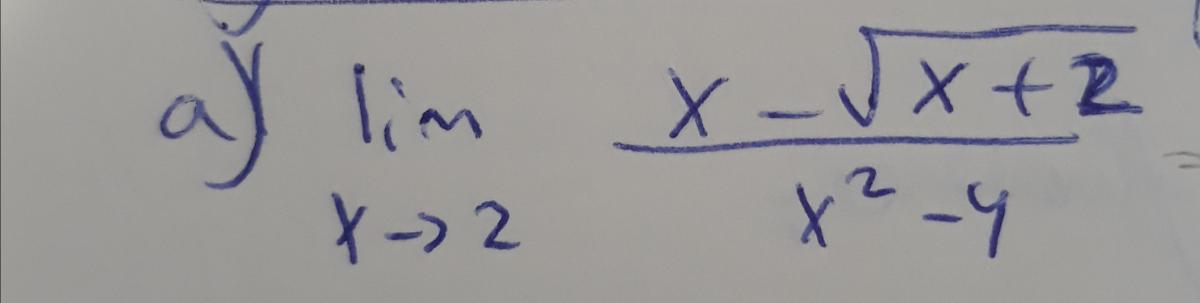
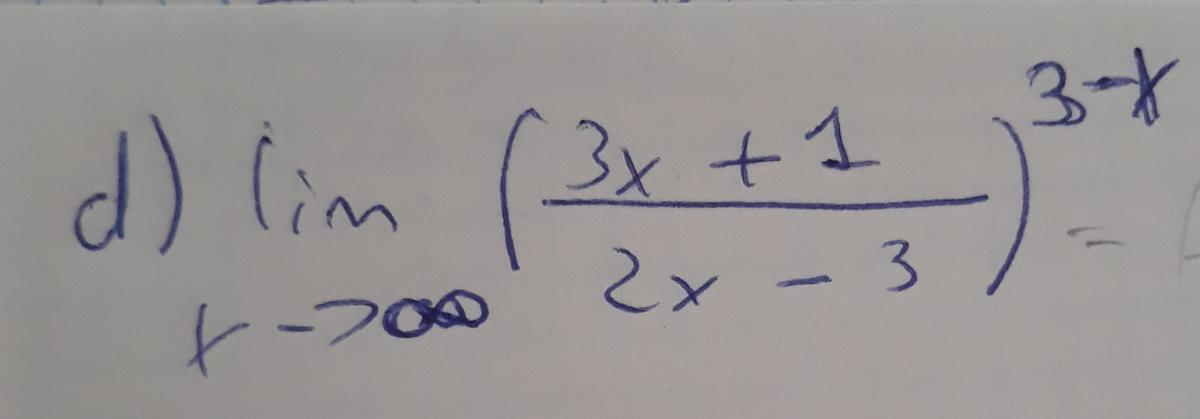
Fermat
el 19/6/18Esta es la gráfica de la segunda función donde se puede apreciar que a medida que x aumenta, el límite tiende a 0 superiormente (0+) :
Y estos son los códigos de matlab con los que puedes resolver cualquier límite (resoluble) y graficarlo posteriormente para comprobar la solución. Es la manera de aprender!! Un saludo.
-
David
el 21/6/18¿Has visto estos vídeos?... Logaritmos
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Antonio Silvio Palmitano
el 18/6/18Puedes comenzar por expresar a las bases de las potencias como exponenciales:
(elnx)y = (elny)x;
aplicas la propiedad de una potencia cuya base es otra potencia en ambos miembros, y queda:
ey*lnx = ex*lny;
derivas implícitamente con respecto a x en ambos miembros (observa que debes aplicar la Regla de la Cadena), y queda:
ey*lnx * ( y ' * lnx + y/x ) = ex*lny * ( lny + x* y '/y );
distribuyes en ambos miembros, y queda:
ey*lnx * y ' *lnx + ey*lnx * y/x = ex*lny * lny + ex*lny * x*y '/y;
restas ey*lnx * y/x y restas ex*lny * x*y '/y en ambos miembros de la ecuación, y queda:
ey*lnx * y ' *lnx - ex*lny * x*y '/y = ex*lny * lny - ey*lnx * y/x;
Extraes factor común en el primer miembro, y queda:
y ' * ( ey*lnx * lnx - ex*lny * x/y ) = ex*lny * lny - ey*lnx * y/x;
divides en ambos miembros de la ecuación por ( ey*lnx * lnx - ex*lny * x/y ), y queda:
y ' = ( ex*lny * lny - ey*lnx * y/x ) / ( ey*lnx * lnx - ex*lny * x/y ),
con las condiciones: x > 0 e y > 0.
Espero haberte ayudado.
Erick Zambrana
el 18/6/18y se puede hacer del método aplicando directamente logaritmo natural? algo asi me sale
yLnx=xLny
y'Lnx+yLn(1/x)=Lny+xLn(y'/y)
y'Lnx-xLn(y'/y)=Lny-yLn(1/x)
el problema me va aca, no se como factorizar y' cuando esta dentro del Ln, en mi examen lo factorice asi:
y'(Lnx-xLn(1/y)) pero mi profe me puso mala nota, o acaso no se puede sacar el factor común cuando y' esta dentro del logaritmo natural ?¿
ESPERO que me pueda ayudar por favor. gracias
Antonio Silvio Palmitano
el 18/6/18Vamos con tu idea, que es una forma equivalente a la anterior.
Tomas logaritmos naturales en ambos miembros, y queda:
ln(xy) = ln(yx),
aplicas la propiedad del logaritmo de una potencia en ambos miembros, y queda:
y*lnx = x*lny,
derivas implícitamente con respecto a x (observa que debes aplicar la regla del producto, y la regla de la cadena en el último factor, y queda:
y ' * lnx + y*(1/x) = 1*lny + x*(1/y)*y ',
restas y*(1/x) y restas x*(1/y)*y ' en ambos miembros, y queda:
y ' * lnx - x*(1/y)*y ' = lny - y*(1/x),
extraes factor común en el primer miembro, resuelves términos, y queda:
y ' * (lnx - x/y) = lny - y/x,
divides en ambos miembros por (lnx - x/y), y qued:
y ' = ( lny - y/x ) / (lnx - x/y),
con las condiciones: x > 0 e y > 0.
Espero haberte ayudado.