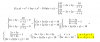-
-
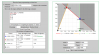
una industria de productos lácteos produce crema de queso de oveja en envases de dos tamaños, pequeño de 100 gramos con un beneficio de envase de 0,50€ y de grandes de 300 gramos con un beneficio de 1.40€. cada día dispone de 2400kg de crema de queso para envasar. por razones de mercado el número de envases de 100 gramos producidos diariamente no puede ser mayor de 15000 y debe ser igual o superior al de envases de 300 gramos.
A: ¿cuántos envases de cada tipo han de producirse diariamente para hacer los máximos beneficios?
La función objetivo sé que es: B:0,50x+1,40y
-
Saludos. Por favor si alguien me puede ayudar con este problema y gracias desde ya a quien me ayude😊. P.D. yo traté de hacerlo con esa fórmula, no se si será correcta.



Antonio Silvio Palmitano
el 3/6/18Planteas un sistema con las ecuaciones de las rectas L1 y L2, y queda:
2x + 3y + 5 = 0 (1),
5x - 2y = 16 (2);
luego, sumas 2y en ambos miembros de la ecuación señalada (2), y queda:
5x = 2y + 16, divides en todos los términos de la ecuación por 5, y queda:
x = (2/5)y + 16/5 (3);
luego, sustituyes la expresión señalada (3) en la ecuación señalada (1), y queda:
2( (2/5)y + 16/5 ) + 3y + 5 = 0, distribuyes el primer término, y queda:
(4/5)y + 32/5 + 3y + 5 = 0, multiplicas por 5 en todos los términos de la ecuación, y queda:
4y + 32 + 15y + 25 = 0, reduces términos semejantes, y queda:
19y + 47 = 0, restas 47 en ambos miembros de la ecuación, y queda:
19y = -57, divides por 19 en ambos miembros de la ecuación, y queda: y = -3;
luego, reemplazas el valor remarcado en la ecuación señalada (3), y queda
x = (2/5)(-3) + 16/5, resuelves y queda: x = 2;
por lo que tienes que el punto de intersección de la recta L1 con la recta L2 es: A(2,-3).
Luego, tienes la ecuación de la recta cuya pendiente debes determinar:
y + 4 = m(x + 8) (4), reemplazas las coordenadas del punto A que pertenece a esta recta, y queda:
-3 + 4 = m(2 +8), resuelves operaciones entre números, y queda:
1 = m(10), divides por 10 en ambos miembros de la ecuación, y queda: 1/10 = m;
luego, reemplazas el valor de la pendiente que hemos remarcado en la ecuación de la recta buscada señalada (4), y queda:
y + 4 = (1/10)(x + 8), distribuyes el segundo miembro, y queda:
y + 4 = (1/10)x + 4/5, restas 4 en ambos miembros, y queda: y = (1/10)x - 16/5,
que es la ecuación cartesiana explícita de la recta que te piden en tu enunciado.
Espero haberte ayudado.
-
Hola buenas tardes, a ver si me podrían echar una cable:
Programación lineal :
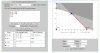
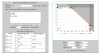
Un talle de confección textil produce dos categorías de trajes de señora y de caballero.Dispone de material para fabricar diariamente 850 trajes de señora y de 650 de trajes caballero. si tiene que fabricar diariamente como máximo 1000 unidades totales y el beneficio obtenido por cada traje de señora es de 150 euros y de 200 euros por traje de caballero, se pide :
(a) ¿Cuántos trajes de cada tipo han de fabricarse diariamente para hacer máximo beneficio?
(b) el valor de dicho beneficio máximo.