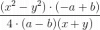-
Hola necesito que me ayudéis a comprender como ha llegado al resultado (paso a paso)
Muchas gracias adelantadas!!!
Antonio Silvio Palmitano
el 16/5/18Tienes la expresión del segundo miembro de tu cadena de igualdades:
(x/n)*( (1-ex)/(1-ex/n) ) =
resuelves el producto entre fracciones, y queda:
= ( x*(1-ex) ) / ( n*(1-ex/n) ) =
conmutas los factores en el numerador, y queda:
= ( (1-ex)*x ) / ( n*(1-ex/n) ) =
expresas a la fracción como un producto de fracciones, y queda:
= ( (1-ex)/1 )*(x/n)*(1/(1-ex/n) =
omites el denominador en el primer factor, y queda:
= (1-ex)*( x/n)*(1/(1-ex/n) =
resuelves la multiplicación de los dos últimos factores, y queda:
= (1-ex)*( (x/n)/(1-ex/n) ).
Luego, planteas el límite, y queda:
Lím(n→+∞) (1-ex)*( (x/n)/(1-ex/n) ) =
extraes el primer factor (observa que no depende de la variable n), y queda:
= (1-ex) * Lím(n→+∞) ( (x/n)/(1-ex/n) ) =
planteas la sustitución (cambio de variable): x/n = w (observa que w tiende a cero desde valores positivos cuando n tiende a +infinito), y queda :
= (1-ex) * Lím(w→0+) ( w/(1-ew) ) =
aquí, en conversación con el Colega Guillem de la Calle Vicente, hemos acordado que debe hacerse la aclaración que extendemos la expresión a los números reales, luego aplicas la Regla de L'Hôpital en el límite, y queda:
= (1-ex) * Lím(w→0+) ( 1/(-ew) ) =
resuelves el límite, y queda:
= (1-ex) * (-1) =
distribuyes el factor común, y queda:
= -1 + ex =
conmutas términos, y queda:
= ex - 1.
Espero haberte ayudado.
-
Hola, necesito ayuda con este ejercicio: . Se han comprado tres productos A, B y C. Sin tener en cuenta el IVA, el producto C vale 360€ menos que la suma de lo que cuestan A y B conjuntamente, mientras que el importe total de los tres productos asciende a 800 €. El producto A paga un IVA del 6%, el producto B del 12% y el producto C del 30%. La factura total con IVA importa 917,60€. a) Plantear un sistema de ecuaciones para calcular la cantidad, sin IVA, que cuesta cada producto. b) Resolver el sistema por el método de Cramer.
Gracias.
Luis Morales
el 16/5/18Hola, me parece que tiene un problema de lenguaje matemático.
Tienes que buscar cada una de las ecuaciones en el enunciado.
Te voy a indicar la primera y tienes que buscar las otras dos:1.- "Sin tener en cuenta el IVA, el producto C vale 360€ menos que la suma de lo que cuestan A y B conjuntamente"
C-360 = A+B
Donde: A precio sin IVA del PRODUCTO AB precio sin IVA del PRODUCTO B
C precio sin IVA del PRODUCTO CTe animo a que busques las otras dos ecuaciones en el enunciado.Antonio Silvio Palmitano
el 16/5/18Llamamos A, B, C a los precios sin IVA de los productos respectivamente
Luego, los precios con IVA quedan, respectivamente:
A + 0,06*A = 1,06*aA,
B + 0,12*B = 1,12*B,
C + 0,30*C = 1,30*C.
Luego, tienes las proposciones:
a)
"C es menor en 360 euros a la suma de A más B", por lo que puedes plantear la ecuación:
C = A + B - 360, restas A y restas B en ambos miembros, y queda:
-A - B + C = -360, multiplicas por -1 en todos los términos de la ecuación, y queda:
A + B - C = 360 (1).
b)
"El importe total de los tres productos es 800 euros", por lo que puedes plantear la ecuación:
A + B + C = 800 (2).
c)
"La factura total con IVA importa 917,60 euros", por lo que puedes plantear la ecuación:
1,06*A + 1,12*B + 1,30*C = 917,60,
multiplicas por 100 en todos los términos de la ecuación, y queda:
106*A + 112*B + 130*C = 91760,
divides por 2 en todos los términos de la ecuación, y queda:
53*A + 56*B + 65*C = 45880 (3).
Luego, con las ecuaciones señaladas (1) (2) (3) tienes un sistema de tres ecuaciones lineales, de primer grado y con tres incógnitas, que debes resolver por medio de la Regla de Cramer.
Haz el intento de terminar la tarea, y si te resulta necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
Luis Morales
el 16/5/18Adrian Pisabarro García
el 16/5/18 -
ayuda por favor
En un estadio se hace una encuesta sobre la marcha del equipo local. Se pregunta a 600 aficionados y 225 contestan que la marcha no es buena. Obtener con un nivel de significación del 5% un intervalo de confianza para la proporción de aficionados que piensan que el equipo está mal
. a) (0,336; 0414) b) (0; 0,336) c) (0,414; 0,741)
-
ayuda por favor
Una entidad bancaria predice los beneficios futuros, en miles de millones de euros, mediante la función
𝐵(𝑡) = 5𝑡 / 𝑡+3 (− 2)
donde t son los años
¿Hacia qué valor tiende el beneficio?
a) 5000 millones de euros.
b) Con la información suministrada no se puede saber.
c) 3000 millones de euros.
Luis Morales
el 16/5/18 -
ayuda con esta inecuacion por favor :D
Determinar si los valores 𝑥 = 2 y 𝑥 = 0 son soluciones de la inecuación 3𝑥+2 / 𝑥−1 ≥ 𝑥−4 / 7+2
Luis Morales
el 16/5/18