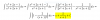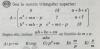-
mari carmen
el 23/3/18 -
Andres Sampayo
el 23/3/18Perdonen si he molestado mucho pero solo necesito ayuda con la integral de esta última función
((X^2)+(2x)-1)/((x^2)+(2x)+1)
-
Héctor
el 23/3/18 -
Andres Sampayo
el 23/3/18 -
Aitor
el 23/3/18 -
Andres Sampayo
el 23/3/18Alguien me podría ayudar con la simplificación y solución de esta ecuación
(Y^3)+6(Y^2)+Y-34=0
Antonio Silvio Palmitano
el 23/3/18Observa que y = 2 es una solución de la ecuación. Luego, divides el polinomio del primer miembro por (y-2) con la Regla de Ruffini, factorizas, y queda:
(y - 2)*(y2 + 8y + 17) = 0.
Luego, por anulación de un producto, tienes dos opciones:
a)
y - 2 = 0, sumas 2 en ambos miembros, y queda: y = 2;
b)
y2 + 8y + 17 = 0,
que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente, y queda:
y = ( -8 ± √(-4) )/2, que no es un número real.
Luego, si estás trabajando en el conjunto de los números reales, tienes que la única solución de la ecuación es:
y = 2.
Pero, si estás trabajando en el conjunto de los números complejos, tienes las soluciones adicionales:
y = ( -8 ± 2*i )/2 = - 4 ± i,y por lo tanto quedan: y = -4 + i e y = -4 - i.
Luego, si estás trabajando en el conjunto de los números complejos, tienes que las tres soluciones de la ecuación son:
y = 2,
y = -4 + i,
y = -4 - i.
Espero haberte ayudado.
-
Zero X
el 23/3/18
Podrias ayudarme por favor
Antonius Benedictus
el 23/3/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Diego Mauricio Heredia
el 23/3/18 -
Antonio Silvio Palmitano
el 23/3/18Pregunta de mauriciomolin@gmail.com en el chat de Matemática.
Verificar la siguiente identidad trigonométrica:
(tga+tgb)/(tga-tgb)=sen(a+b)/sen(a-b) .
Comienza por desarrollar el numerador (N) y el denominador (D) del primer miembro en función de seno y del coseno:
N = tana + tanb = sena/cosa + senb/cosb = (sena*cosb + cosa*senb) / cosa*cosb =
aplicas la identidad del seno de la suma de dos ángulos en el numerador, y queda:
= sen(a+b) / cosa*cosb (1).
D = tana - tanb = sena/cosa - senb/cosb = (sena*cosb - cosa*senb) / cosa*cosb =
aplicas la identidad del seno de la resta de dos ángulos en el numerador, y queda:= sen(a-b) / cosa*cosb (2).
Luego, planteas la expresión del primer miembro de la identidad:
(tga +tgb) / (tga - tgb) = sustituyes las expresiones señaladas (1) (2), y queda:
[sen(a+b) / cosa*cosb] / [sen(a-b) / cosa*cosb] = simplificas los denominadores de los agrupamientos, y queda:
= sen(a+b) /sen(a-b).
Espero haberte ayudado.
