-
Lsslie
el 21/3/18 -
Nicolas
el 21/3/18Hola! Una pregunta, como tendría que resolver el punto c y d ??
Se considera una muestra de 200 personas para realizar un estudio sobre los niveles de colesterol a los 40 años de edad. Esto se considera de forma creciente por intervalo de clases y se muestran en la siguiente tabla.
Ángel
el 21/3/18El c) y el d) los solucionas con la fórmula del percentil de un número k.
Pk= Li+ Ai*( ((k*n)/100)-Fi-1 )/fi ,
con j=0,......,98,99 , Li=Límite inferior de la clase del percentil k, Ai=Amplitud de los intervalos, n=nº de observaciones,
Fi-1=Frecuencia acumulada en el intervalo anterior, fi =Frecuencia en el intervalo
c)
Primero vemos el intervalo donde se va a encontrar P25 :
(25*200)/100= 50 (entonces se encontrará en [170,190), porque Fi-1=10 y Fi+1=65)
APLICANDO LA FÓRMULA:
P25= 170+ 20*( ((25*200)/100)-10 )/55
P25= 170+ 20*( 50-10 )/55
P25= 170+ (800/55)
P25= 170+ (160/11)
P25= (1870+160)/11
P25= 2030/11
P25≈ 184.5454545454...
Entonces los que estén por debajo del percentil 25 estarán por debajo de 184.5454 mg de colesterol ÷ 100 ml de sangre
-
Ramon Paillalevie
el 21/3/18alguien me puede dar una manito con este ejercisio 3x-1=6(x/2+5)
David Poyatos
el 21/3/18 -
ivan
el 21/3/18no se como hacer el ejercicio 5, el señalado
Antonio Silvio Palmitano
el 21/3/18Observa que el dominio de la función es: D = (-∞,1) u (1,+∞).
Observa que tienes un valor de corte entre trozos: x = 2.
a)
Plantes la definición de continuidad de una función en el punto de corte x = 2:
1°)
f(2) = (2+2)/(2-1) = 4/1 = 4;
2°)
Lím(x→2-) f(x) = Lím(x→2-) (x+2)/(x-1) = 4/1 = 4,
Lím(x→2+) f(x) = Lím(x→2+) (3x2-2x)/(x+2) = 8/4 = 2,
por lo que tienes que el límite de la función para x tendiendo a 2 de la función no existe;
3°)
la función es discontinua esencial (o inevitable) en x = 2, y su gráfica presenta un salto en dicho valor.
b1)Lím(x→-∞) f(x) = Lím(x→-∞) (x+2)/(x-1) = Lím(x→-∞) x(1+2/x) / x(1-1/x) = Lím(x→-∞) (1-2/x)/(1-1/x) = 1/1 = 1,
por lo que tienes que la gráfica de la función presenta asíntota horizontal izquierda, cuya ecuación es:
y = 1 y, por lo tanto, tienes que la gráfica de la función no presenta asíntota oblicua izquierda;
b2)
Lím(x→+∞) f(x) = Lím(x→+∞) (3x2-2x)/(x+2) = Lím(x→+∞) x2(3-2/x) / x(1+2/x) =
= Lím(x→+∞) x(3-2/x)/(1+2/x) = +∞,
por lo que tienes que la gráfica de la función no presenta asíntota horizontal derecha;
b3)
Lím(x→+∞) f(x)/x = Lím(x→+∞) (3x2-2x) / x(x+2) = Lím(x→+∞) x2(3-2/x) / x2(1+2/x) =
= Lím(x→+∞) (3-2/x)/(1+2/x) = 3,
por lo que la pendiente de la asíntota oblicua derecha sería: m = 3,
Lím(x→+∞) (f(x) - mx) = Lím(x→+∞) ( (3x2-2x)/(x+2) - 3x ) = Lím(x→+∞) ( 3x2-2x - 3x(x+2) ) / (x+2) =
= Lím(x→+∞) (3x2-2x - 3x2-6x) / (x+2) = Lím(x→+∞) (-8x) / (x+2) =
= Lím(x→+∞) (-8x) / x(1+2/x) = Lím(x→+∞) (-8) / (1+2/x) = -8,
por lo que tienes que la ordenada al origen de la asíntota oblicua derecha es b = -8,
y puedes concluir que la gráfica de la función presenta asíntota oblicua derecha, cuya ecuación cartesiana explícita es:
y = 3x - 8.
Espero haberte ayudado.
-
Lsslie
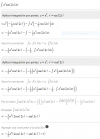
el 21/3/18Hola, para hacer este ejercicio de integrales: Encuentra la primitiva de la función f(x)= -x / 1-x^2 cuya gráfica pasa por el punto de coordenadas A(√2 , 3) , lo que tengo que hacer es la integral de f(x) y despues f(√2) = 3 ??? Gracias !!!
-
ivan
el 21/3/18 -
Sumi
el 21/3/18
buenass, me podría alguien decir que error tengo, porque el area me sale negativo...Muchas gracias 😊 -
Verónica Ortiz
el 21/3/18Hola,
me gustaria saber como hayar en un triangulo cualquiera, las razones trigonometricas. (4ºESO) No comprendo bien como saber hacerlo.
César
el 21/3/18 -
ViRR
el 21/3/18Buenas tardes, no sé cómo resolver el siguiente ejercicio, ¿podrían ayudarme?
Se quiere construir una piscina en forma de paralelepípedo recto de base cuadrada. Disponemos de 192 m2 de baldosas para recubrir las paredes y el fondo de la piscina. Halla las dimensiones de la piscina de manera que su capacidad sea máxima.
¡Muchas gracias!
-
Verónica Ortiz
el 21/3/18
