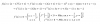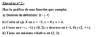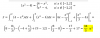-
carmela
el 21/3/18Buenos días. He comprado el ebook recopilatorio de ejercicios de matemáticas para la PAU. Me está siendo de gran utilidad, no solo para prepararla, sino también para exámenes del curso. No sabía donde ponerlo, así que desde aquí doy la enhorabuena a los culpables.
-
marwin yepez
el 21/3/18Hola buenas espero puedan ayudarme con este ejercicio de estatistica por mas que trato de hacerlo no puedo... intente hacerlo y me daba 17.88 no si si el resultado estara bueno... Una máquina llena recipientes con determinado producto. Se sabe que la desviación estándar de pesos de llenado, de acuerdo con datos históricos, es de 0.6 onzas. Si sólo 2% de los recipientes contienen menos de 18 onzas y suponiendo que los pesos de llenado tienen distribución normal. Determine: a. El peso promedio de llenado. δ= 0.6 µ= ? Z= .02 X = 18
-
Andres Sampayo
el 21/3/18 -
Jonathan Yañez
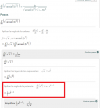
el 21/3/18---------------- DERIVADA ----------------
PROBLEMA: No entiendo porque en la parte que enmarque con rojo no multiplica también por (u)'
teniendo en cuenta esta formula f(x)=u^n--->f'(x)=n(u^(n-1))(u)' Ademas, u en este caso representa
el arcsen(5x^2). Si fuera x lo entendería, porque al derivar x, obtengo (1)(x^(1-1))(x)', lo cual me da 1
y no me cambia nada al multiplicar, pero en este caso es distinto.
-
Cristina Cris Silka
el 20/3/18Hola, me contralarian el siguiente ejercicio para saber si esta bien ( los resolvi con teorema de Gauss, en el d) no encontre raices posibles)
Factoriza los siguientes polinomios:
a) P(x) = 3x^2 - 10x + 3
b) Q(x) = 2x^2 -x - 1
c) T(x)= x^3 - 4x^2 + 4x
d) M(x) = x^3 - 2x^2 - x -2
Rasyer
el 21/3/18En el c) podrías haber llegado un poco más lejos.
La descomposición es x³ - 4x² + 4x = (x² -2x) * (x - 2) = x * (x - 2) * (x - 2) = x * (x-2)²
Una pequeña aclaración antes del d), las posibles soluciones que tu tienes apuntadas son únicamente racionales, o sea, pueden haber soluciones irracionales que no podamos calcular con este método.
Dicho esto la d) no tiene soluciones racionales, aunque si tiene una solución real. Esto lo se porque he representado la función. Revisa el enunciado, ya que es raro que pongan este tipo de polinomio.
Te dejo la representación gráfica del d:
https://es.symbolab.com/solver/polynomial-calculator/x%C2%B3%20-%20%20x%5E%7B2%7D-2x%20-1
-
Cristina Cris Silka
el 20/3/18Hola, me podrían controlar el siguiente ejercicio para saber si esta bien:
Hallar la pendiente y la ordenada de origen de las siguientes rectas:
a) x + y = 3 b) x - 6 = 3y c) 2y + x = 2
Como los resolví:
a) x + y = 3 b) x - 6 = 3y c) 2y + x = 2
x= 3 - y x= 3y + 6 x = 2 -2y
Pendiente: 3 Pendiente : 6 Pendiente: 2
Ordenada de origen: - y Ordenada de origen: 3y Ordenada de origen: -2y
David Poyatos
el 20/3/18Como todas las ecuaciones se encuentran en la forma explícita de la recta: y=mx+n. Donde m (coeficiente de la x) es la pendiente de la recta y n es la ordenada en el origen.
Los apartados a, b y c están mal resueltos `porque hay que dejarlos en y=mx+n
En el apartado a: y=-x+3 ----> donde m=-1 y n= 3
En el apartado b: y=(1/3)x-2 ----> donde m=1/3 y n=-2
En el apartado c: y=(-1/2)x +1----> donde m=-1/2 y n=1
Espero haberte ayudado.
-
Sumi
el 20/3/18 -
Hafssa
el 20/3/18hola.Porfavor quien me puede explicar como hacer este ejercicio no lo entiendo .y graacias
David Poyatos
el 20/3/18Para sacar que tiene un máximo relativo en P(2,3) lo que haces es hayar las derivadas primera y segunda de la función que te den. Una vez hayada la primera, la igualas a 0 y te darán uno o más valores en función de las soluciones que tenga la derivada primera, después esos valores los sustituyes en la derivada segunda y si te dan > 0 es un mínimo y se te da < 0 es un máximo.
Luego el valor que te haya dado lo sustituyes en la función sin derivar y te dará el valor de la y del máximo o mínimo.
En este caso, el ejercicio lo que te dice es que f'(x)=0 en x=2 y f"(2)<0 y f(2)=3 . Teniendo elaximo relativo en P(2,3).
Espero haberte ayudado
David Poyatos
el 20/3/18 -
Lsslie
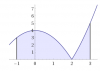
el 20/3/18Hola, me ayudan con este ejercicio porfavor: Determina los puntos de intersección, si existen, entre las funciones f(x) = 8/x y g(x) = √x . Calcula el área del recinto comprendido entre estas dos funciones y la recta x=8 . Gracias !!!
Antonio Silvio Palmitano
el 20/3/18Plantea la condición de intersección entre las gráficas de las funciones:
g(x) = f(x), sustituyes expresiones, y queda:
√(x) = 8/x,
observa que x debe tomar valores estrictamente mayores que cero, elevas al cuadrado en ambos miembros, y queda:
x = 64/x2, multiplicas por x2 en ambos miembros, y queda:
x3 = 64, extraes raíz cúbica en ambos miembros, y queda:
x = 4;
luego, evalúas las expresiones de las funciones, y para ambas tienes que toman el valor y = 2,
por lo que las gráficas se cortan en el punto (4,2).
Luego, observa que para x = 8 tienes que las funciones toman los valores: f(8) = 1 y g(8) = √(8),
por lo que tienes que otros vértices de la región son los puntos (8,1) y (8,√(8)).
Luego, evalúas para un valor intermedio entre las abscisas de los vértices, por ejemplo x = 5, evalúas las expresiones de las funciones, y queda:
f(5) = 8/5 = 1,6,
g(5) = √(5) ≅ 2,236,
por lo que tienes que la gráfica de la función g es "más alta" que la gráfica de la función f en un gráfico cartesiano.
Luego, planteas la expresión del área del recinto:
A = 4∫8 ( √(x) - 8/x )*dx = 4∫8 ( x1/2 - 8*x-1 )*dx,
integras, y queda:
A = [ (2/3)*x3/2 - 8*lnx ], evalúas, y queda:
A = ( (2/3)*83/2 - 8*ln8 ) - ( (2/3)*43/2 - 8*ln4 ).
Luego, solo queda que hagas el cálculo.
Espero haberte ayudado.
-
Ashley
el 20/3/18
