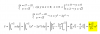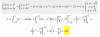-
Hoola me pueden ayudar con este ejercicio?? Gracias !!
La funcion f(x) = Inx , el eje de abscisas y la recta x = e limitan un recinto finito en el plano. Halla su área mediante el cálculo integral.
Antonio Silvio Palmitano
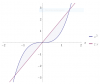
el 20/3/18Haz un gráfico, y observa que tienes una región parecida a un triángulo con vértices: (1,0), (e,0) y (e,1),
que está limitada inferiormente por un segmento incluido en el eje OX cuyos extremos son: x = 1 y x = e,
y superiormente por un trozo de la curva logarítmica cuyos extremos son los puntos (1,0) y (e,1),
que tienen sus abscisas comprendidas entre x = 1 y x = e.
Luego, tienes que la curva que limita superiormente a la región tiene ecuación: y = lnx,
y que la curva que la limita inferiormente (el eje OX) tiene ecuación: y = 0.
Luego, planteas para el área de la región:
A = 1∫e (lnx - 0)*dx = 1∫e lnx*dx;
luego, aplicas el Método de Integración por Partes (u = lnx, du = dx/x, dv = dx, v = x), y queda:
A = [ x*lnx - x ], para evaluar con Regla de Barrow entre x = 1 y x = e;
luego, evalúas, y queda:
A = (e*lne - e) - (1*ln1 - 1), resuelves los logaritmos, y queda:
A = (e*1 - e) - (1*0 - 1) = resuelves multiplicaciones = (e - e) - (0 - 1) = 0 - (-1) = 1.
Espero haberte ayudado.
Lsslie
el 21/3/18Antonio Silvio Palmitano
el 21/3/18Observa que tienes las gráficas:
(1) y = lnx (que corresponde a la función),
(2) y = 0 (que corresponde al eje de abscisas OX,
y tienes también la ecuación de la recta paralela al eje OY:
(3) x = e.
Luego, planteas las intersecciones, igualando expresiones dos a dos:
1°)
lnx = 0, compones en ambos miembros con la función inversa del logaritmo natural, y queda:
x = 1, por lo que tienes que las gráficas (1) y (2) se cortan en el punto: A(1,0);
2°)
sustituyes el valor señalado (3) en la ecuación señalada (1), y queda:
y = ln(e) = 1, por lo que tienes que la gráfica (1) y la recta (3) se cortan en el punto: B(e,1);
3°)
observa los valores señalados (2) (3), y tienes que la gráfica (2) y la recta (3) se cortan en el punto: C(e,0).
Luego, observa que solo "hemos igualado a cero" en el primer caso, cuando planteamos la intersección de la gráfica de la función con el eje OX.
Espero haberte ayudado.
-
Hola, tengo algunas dudas con el siguiente ejercicio:
Resolver la siguiente situación problemática:
a) Una compañía de telefonía móvil cobra a sus clientes una cantidad fija al mes de $100 más $10 por cada minuto de llamada. Construir una tabla que relacione el tiempo consumido y el coste de la factura . ¿Cuál es la variable independiente y cuál la dependiente ? Gráfica esos datos en un par de ejes cartesianos?
Como intente resolverlo:
f(x) = 100x +10 y variable independiente = 100 Variable dependiente =10
Antonio Silvio Palmitano
el 20/3/18Puedes denominar:
x: tiempo consumido en las llamadas, expresado en minutos (min).;
y: coste total, expresado en pesos ($).
Luego puedes plantear que el coste total es igual a la suma del coste fijo ($ 100) más el coste de las llamadas (10*y, expresado en pesos), y su expresión queda:
y = 100 + 10*x,
donde x es la variable independiente, e y es la variable dependiente.
Luego, observa que x puede tomar solamente valores positivos, por lo que la gráfica es una semirrecta, cuyo primer punto es (0,100), y otro de sus puntos es (1,110)
Luego, solo queda que hagas el gráfico cartesiano.
Espero haberte ayudado.
-
Hola, estoy algo atascada en un ejercicio de circunferencias, me podrías echar una mano porfavor
calcula el valor de B de modo que la recta sea 3x + By - 6 = 0 sea tangente a la circunferencia x elevado al cuadrado + y elevado al cuadrado + 10x + 2y + 1 = 0
GRACIAAS
-
Hola, estoy atascada en una factorizacion de polinomios. Me pide descomponer en factores, pero no me sale.
4(x+y)^2 + 1/16 + x + y
Gracias.
Antonio Silvio Palmitano
el 20/3/18Puedes ordenar términos, escribir al término cuadrático como una potencia, y queda:
( 2(x+y) )2 + (x+y) + 1/16.
Luego, puedes escribir al último término como un cuadrado, agregas el coeficiente neutro en el segundo término, y queda:
( 2(x+y) )2 + 1*(x+y) + (1/4)2.
Luego, escribes al coeficiente del segundo término como una multiplicación, y queda:
( 2(x+y) )2 + 2*2*(1/4)*(x+y) + (1/4)2.
Luego, factorizas el trinomio cuadrado perfecto, y queda:
( 2(x+y) + 1/4 )2 = (2x + 2y +1/4)2.
Espero haberte ayudado.
-
Buenas, estoy haciendo un repaso del curso para selectividad y hay un ejercicio de calculo de areas con integrales no me sale, el ejercicio dice lo siguiente: Encuentra el area de la zona limitada por las funciones f(x)= x^3 i g(x)= 2x. La solucion es 2u^2.
Gracias!! -
Hola, estoy dando derivadas en clase y hay otro ejercicio que no sé derivar. El enunciado del ejercicio es: Representa (boceto) y analiza las siguientes funciones (dominio, asintota y los cortes de los ejes)
f(x)= log1/3 X
f(x)= 3X
Gracias
Inés
el 20/3/18Hola, tengo varias dudas:
Cuando haces el: x=(1/3)0 cuando nos encontramos una operación con LOG que se tenga que hacer así, se pone el 0 ?
Cuando se buscan los limites, porque acaba poniendo x-> infinito y no x->0-? Y me he perdido a partir de ese paso
Y cuando haces la derivada, no debería de ser xln (3-1)?
Guillem De La Calle Vicente
el 20/3/18el x=(1/3)^0, lo hago para mirar si la función corta con el eje x, que tenemos y=0. Luego, tenemos 0 = log_{1/3}(x) que para resolver esta ecuación logarítmica, aplico la función inversa del log_{1/3)(x) que es el (1/3)^x, y por tanto (1/3)^0. No siempre se pone el elevado a 0, ni mucho menos. En este caso sí, pero no es común.
Cuando hago los límites, estoy analizando si existen asíntotas y ver cuáles son. Recuerda que para ver si hay asintotas horizontales, tienes que estudiar los límites cuando x tiende a más o menos infinito y si da un número k, pues y=k será una asíntota horizontal. Como que da infinito, no hay asintota horizontal. Solo lo hago para el más infiintio, porque la función no está definida para menos infinito. Luego para calcular la asíntota vertical se tiene que considerar los puntos que no pertenecen al dominio de la función y pienses que pueden formar una infinita. En este caso, solo el 0^+, porque todos los otros puntos que no pertencen al dominio, la función no tendrá sentido para estos y por tanto no hace falta verlo. Luego se tiene que hacer el lim cuando x tiende a 0^+ y como que da infinito, x=0 es una asintota horizontal. Y para ver si hay asintotas oblicuas y=mx+n, con m = lim_{x\to \infty} f(x)/x, y n=lim_{x\to \infty} [f(x)-mx]. El primer límite da 0, y podríamos pensar que existe, pero luego la n sería el límite al infinito de f(x) que ya hemos visto que da infinito, por tanto no existen.
Y luego, la parte de las derivadas, es una parte fácil del estudio de una función. Tienes que estudiar los puntos críticos, el signo de la primera derivada, de la segunda, etc. La derivada de log_a(x) es 1/(x*ln(a)), en este caso: 1/(x*ln(1/3)) que es lo mismo que 1/(x*ln(3^(-1)). Luego tenemos que 1/(-x*ln(3)) por las propiedades del logaritmo, y entonces ya hay lo que he puesto: -1/(x*ln(3)).
Saludos.
-
Hola, estoy dando derivadas en clase y hay un ejercicio que no sé derivar. El enunciado del ejercicio es: Concepto de derivadas, calculo de funciones derivadas y derivadas en un punto)
f(x)= (ex+1)2
f(x)= log3 (1+2x-x3)
f(x)= ln∛x2
Gracias
Raúl RC
el 21/3/18La idea consiste en derivar de fuera hacia adentro.
Para la primera función tendrás:
f(x)=(ex+1)2=> f'(x)=2(ex+1)·ex
Es decir, primero derivas la potencia y despues multiplicas por la derivada interna (recuerda que hemos de derivar 2 funciones, primero la potencia y luego la exponiencial que es donde se encuentra la variable)
Espero lo entiendas mejor, mírate los videos que te dijo Antonio ;)
-
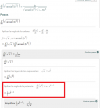
---------------- DERIVADA ----------------
PROBLEMA: No entiendo porque en la parte que enmarque con rojo no multiplica también por (u)'
teniendo en cuenta esta formula f(x)=u^n--->f'(x)=n(u^(n-1))(u)' Ademas, u en este caso representa
el arcsen(5x^2). Si fuera x lo entendería, porque al derivar x, obtengo (1)(x^(1-1))(x)', lo cual me da 1
y no me cambia nada al multiplicar, pero en este caso es distinto.
Antonius Benedictus
el 20/3/18Jonathan Yañez
el 20/3/18Pero no se supone que (1/2)u^(1/2 -1) se debe multiplicar también por (u)' ?
que seria algo así como :
(1/2)u^(1/2 -1)(u)'(1/2)u^(1/2 -1)(arcsen(5x^2))'
Yo lo pregunto basándome en esta formula f(x)=u^n--->f'(x)=n(u^(n-1))(u)'
Eso es lo que no logro comprender, porque no se tiene que realizar en este caso esa multiplicación.
-
¿El vector (0, -2, 0) es igual que el vector (1, -1, 1) ? Creo que leí que puede haber muchos vectores asociados a un autovalor.
Antonius Benedictus
el 20/3/18