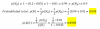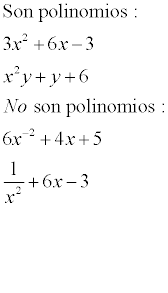-
Hola buenas tardes,
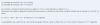
Voy a intentar poner el enunciado de la mejor manera posible para que se pueda entender, ya que no se debió de entender bien: para producir la pieza A se necesitan los componentes A1 y A2. Para que A no sea defectuoso A1 y A2 no deben ser defectuosos. La probabilidad para que dichos componentes sean defectuosos es de 0,2 (A1) y 0,05 (A2). A la vez que se produce la pieza A se produce una pieza B. La probabilidad de que la pieza B no sea defectuosa es de 0,9. (1.) Si en un conjunto de mismas proporciones de la pieza A y la pieza B se escoge una pieza al azar, ¿cuál es la probabilidad para que dicha pieza no sea defectuosa? (2.) Si la pieza que se ha escogido es defectuosa, ¿cuál es la probabilidad que sea una pieza de tipo A?
Muchas gracias.
-
Buenas tardes:
Haciendo el examen correspondinte a ecuaciones de segundo grado y resolución de problemas, me encuentro el siguiente problema:
"Las agujas de un reloj marcan las 6 en punto. ¿A Qué hora volverán las agujas a formar una línea recta?"
Entiendo que está relacionado con los ángulos de las agujas, pero no consigo plantear las ecuaciones.
Agradecería que me echaraís una mano.
Gracias
Ángel
el 19/3/18Agujadelahora------> Recorre 360º en 12 horas, por lo que recorre 30º por hora, por lo que recorre 0.5º/minuto
Agujadelosminutos-->Recorre 360º en 1 hora, por lo que recorre 6º/minuto
Primera línea recta (opuestas) -----> 0.5x+180=6x --> 5.5x=180 --> x= 32,72 minutos después de las 6 en punto
Segunda línea recta (superpuestas) -----> 0.5x+360=6x --> 5.5x=360 --> x= 65,4545 minutos después de las 6 en punto
Entonces:
Primera línea recta ------> A las 6 horas + 32,72 minutos ------> A las 6 horas, 32 minutos, 43 segundos (ayudándote del sistema sexagesimal)
Segunda línea recta -----> A las 7 horas + 5,45 minutos --------> A las 7 horas, 5 minutos, 27 segundos (ídem)
-
4º ESO, por favor me podéis decir si los siguientes ejercicios los he hecho bien, necesito saberlo para poder continuar con otros, o seguir repasando la teoría.
1.- ( x2 −6x+ 5 / x2 +5x+6) • (2x2 −8 / x2 −x) mi resultado: (x− 5)•2(x−2) / x(x+3)
2.- (x4 −2x3 −x+2 / x−1) • (x+2 / x3 −x2 +x−1) mi resultado: (x2 −4)(x2 +x+1) / (x2 +1)(x−1)
3.- (x−1/x) : (x−1/x) mi resultado: ( x +1)
4.- ( (x−1)/(2x+6) ) : ( (x2 −1)/(3x+9) ) mi resultado: ( 3/ 2(x+1) )
Si no están bien, me podríais decir cómo se hacen. Ya he visto todos los vídeos de simplificación, factorización y operaciones combinadas con fracciones algebraicas.
Muchas gracias.
Ángel
el 19/3/18 -
Hola Unicoos. Adjunto este ejercicio y planteo una duda sobre el proceder.
En b) he calculado los vectores asociados para delta y a = 3; y delta y a = 1. Me ha salido los siguientes vectores: (2, 0, 1) y (0, 0, 1)
Para el punto c) ... Estoy haciendo la matriz de Paso, ¿Habría que calcular de nuevo cada uno de los vectores con la letra a, o me vale reutilizando los vectores ya calculados, y calculando solo el vector asociado a "a"?
Aquí sale otro resultado de matriz de Paso: https://matrixcalc.org/es/#diagonalize%28%7B%7Ba,1,0%7D,%7B0,3,0%7D,%7B1,0,1%7D%7D%29 donde salen a en la matriz de Paso. En mi caso no saldrian las a.
¿Son ambos resultados correctos?
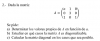
Rasyer
el 19/3/18Hola Sonia,
El problema es que si te dan una matriz con el parámetro a, tienes que calcular tanto los valores propios, los vectores propios y las matrices en función del parámetro a.
En el link que has adjuntado, el vector propio asociado a λ=1, es (0, 0, 1), tal como tu has calculado, pero creo que has cometido algun error calculando el vector propio asociado a λ=3, ya que este es (2, -2a + 6, 1), y en ningun caso es el vector que te ha dado a ti.
Para el c: si usaras los vectores que tu has calculado el resultado sería incorrecto porque estos no son los vectores propios de la matriz original.
Ánimo!
-
Hola soy David y tengo otra duda, pido ayuda, por favor: El cuidador del zoo ha puesto la misma cantidad de leche al lobo y al erizo:3/5 del total. La veterinaria ha sacado 2/7 del total del recipiente del erizo y los ha puesto en el del lobo. ¿Qué fracción del cuenco tendrá ahora cada uno?
Ángel
el 19/3/18Enunciado:
El cuidador del zoo ha puesto la misma cantidad de leche al lobo y al erizo 3/5 del total de cada cuenco. La veterinaria ha sacado 2/7 del total del recipiente del erizo y los ha puesto en el del lobo.
Datos que podemos sacar del enunciado:
El erizo tendrá (3/5 - 2/7) del total de su cuenco.
El lobo tendrá (3/5 + 2/7) del total de su cuenco.
Sumamos/restamos para unificar las fracciones:
3/5 - 2/7 = 21/35 - 10/35 = 11/35
3/5 + 2/7 = 21/35 + 10/35 = 31/35
Conclusiones (solución):
El erizo tendrá 11/35 del total de su cuenco.
El lobo tendrá 31/35 del total de su cuenco.
-
Por favor , soy David Pérez y necesito ayuda con este problema de mates:
En un partido de baloncesto se han metido 100 canastas: 3/5 de 2 puntos, 1/4 de 3 puntos y el resto tiros libres (un punto). ¿Cuántos puntos han marcado en total?
Muchas gracias por la ayuda.
Antonio Silvio Palmitano
el 19/3/18Tienes (3/5)*100 = 60 canastas dobles, que corresponden a: 60*2 = 120 puntos.
Tienes (1/4)*100 = 25 canastas triples, que corresponden a: 25*3 = 75 puntos.
Tienes (1-3/5-1/4)*100 = (3/20)*100 = 15 canastas simples, que corresponden a: 15*1 = 15 puntos.
Luego, tienes para la cantidad total de puntos obtenidos con las cien canastas convertidas:
P = 120 + 75 + 15 = 210.
Espero haberte ayudado.
-
Buenos días.
Ejercicio 1)
Verifica el teorema de green para el campo vectorial F y la región "D" que se indica.
F(x,y)=y î -x j
"D" es la región limitada por el eje "x" además por las parábolas: 4x-y2 +4=0 ; 4x+ y2 - 4=0
Ejercicio 2)
Evaluar la integral de la componente normal de 2xy î - y2 j a lo largo de la elipse definida por (x2/a2) +(y2/b2)=1
Antonius Benedictus
el 19/3/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Tengo una duda para un sistema de ecuaciones el cual es el siguiente (No sé como resolverlo a decir verdad):
(cosθ)x1 + (senθ)x2 =1
(-senθ)x1 + (senθ)x2 =0
Y el siguiente sistema de ecuaciones:
(cosθ)x1 + (senθ)x2 =1
(-senθ)x1 + (senθ)x2 =1
-
Tengo una duda con los polinomios digamos que tengo 3x^0+3x+4 si esta elevado a la 0 es un Polinomio? O digamos que tengo 3/x^2+4x cuando esta en división es un polinomio? Por favor me podrían aclarar esa duda