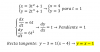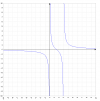
Crecimiento y decrecimiento de una función racional Estudio completo de una funcion racional Representación función racional

Gracias, es el que vi. Pero tengo un problema en la monotonía, al realizar la derivada e igualarla a 0 la raíz cuadrada que me da no tiene solución.

Entonces, carece de extremos relativos (máximos o mínimos).

https://www.unicoos.com/video/matematicas/universidad/algebra/espacios-vectoriales/algebra-base-de-un-espacio-vectorial

log(A/B)=log(A)-log(B)=-(logB-logA)=-log(B/A)

No lo hay, Miriam.

Gracias, Antonio. Seguiré buscando.

Te ayudo con el sistema de ecuaciones.

Tienes la matriz ampliada del sistema:

 0    -1     1     0

-1     1     0     0

 1     0     1     0

Permutas la primera fila con la tercera fila, y queda:

 1     0     1     0

-1     1     0     0

 0    -1     1     0

A la segunda fila le sumas la primera fila, y queda:

1     0     1     0

0     1     1     0

0    -1     1     0

A la tercera fila le sumas la segunda fila, y queda:

1     0     1     0

0     1     1     0

0     0     2     0

A la tercera fila la multiplicas por 1/2, y queda:

1     0     1     0

0     1     1     0

0     0     1     0

A la primera fila le restas la tercera fila, a la segunda fila le restas la tercera fila, y queda:

1     0     0     0

0     1     0     0

0     0     1     0

Luego, tienes el sistema equivalente resuelto:

x = 0,

y = 0,

z = 0,

por lo que tienes que la solución es única y es la solución trivial.

Espero haberte ayudado.

Puedes denominar P y Q a las matrices que tienes en los segundos miembros de las ecuaciones que tienes en tu enunciado.

Luego, tienes el sistema de dos ecuaciones matriciales con dos incógnitas:

2*A + B = P

A - B = Q, aquí sumas B en ambos miembros, y queda: A = Q + B (1);

luego, sustituyes la expresión señalada (1) en la primera ecuación, y queda:

2*(Q + B) + B = P, distribuyes en el primer término, y queda:

2*Q + 2*B + B = P, reduces términos semejantes, y queda:

2*Q +3*B = P, restas 2*Q en ambos miembros, y queda:

3*B = P - 2*Q, multiplicas por 1/3 en todos los términos de la ecuación, y queda:

B = (1/3)*P - (2/3)*Q;

luego, sustituyes la expresión remarcada en la ecuación señalada (1), y queda:

A = Q + (1/3)*P - (2/3)*Q, reduces términos semejantes, y queda:

A = (1/3)*P + (1/3)*Q.

Luego, solo queda que reemplaces las expresiones de las matrices P y Q que tienes en tu enunciado y hagas los cálculos.

Espero haberte ayudado.

Si, muchas gracias!!

Ojo:

- (A/B) = (-A)/B =A/(-B)

O sea que puedo cambiar a cualquiera de los dos pero no a los dos ?? Gracias !!

Considera un sistema de referencia con eje de posiciones OX con origen en la casa de María, con instante inicial (t_i = 0) correspondiente al momento que María sale de su casa.

Recuerda la ecuación de posición de Movimiento Rectilíneo Uniforme:

x = x_i + v*(t - t_i) (*),

donde x_i es la posición inicial del móvil, y t_i es el instante inicial.

Luego, considera el problema en etapas:

1°)

María se desplaza desde su casa hasta la parada del autobús, por lo que tienes los datos iniciales:

t_i = 0, t = 5 min = 5*60 = 300 s,

x_i = 0, x = 200 m,

v₁ = a determinar;

luego, remplazas datos en la ecuación señalada (*), cancelas términos nulos, y queda:

200 = v₁*300, divides por 300 en ambos miembros, y queda: 2/3 m/s = v₁;

luego, reemplazas el valor remarcado y los datos iniciales en la ecuación señalada (*), cancelas términos nulos, y queda:

x = (2/3)*t (en metros), con 0 ≤ t ≤ 300 (en segundos) (1);

2°)

María espera la llegada del autobús:

t_i = 300 s, t = 300 s + 10 min = 300 + 10*60 = 900 s,

x = 200 m (constante),

v₂ = 0;

por lo que la expresión de la función posición queda:

x = 200 (en metros), con 300 ≤ t ≤ 900 (en segundos) (2);

3°)

María se desplaza a pie en camino a su trabajo:

t_i = 900 s, t = 900 s + 1/4 h = 900 + (1/4)*60 = 900 s + 15 min = 900 15*60 = 900 + 900 = 1800 s,

x_i = 200 m, x = 1 Km - 300 m = 1000 - 300= 700 m,

v₃ = a determinar;

luego, remplazas datos en la ecuación señalada (*), y queda:

700 = 200 + v₃*(1800 - 900), resuelves el coeficiente en el último término, y queda:

700 = 200 + 900*v₃, restas 700 y restas 900*v₃ en ambos miembros, y queda:

-900*v₃ = -500, divides por -900 en ambos miembros, y queda: v₃ = 5/9 m/s;

luego, reemplazas el valor remarcado y los datos iniciales en la ecuación señalada (*), cancelas términos nulos, y queda:

x = 200 + (5/9)*(t - 900) (en metros), con 900 ≤ t ≤ 1800 (en segundos) (3);

4°)

María regresa a su casa:

t_i = 1800 s, t = 1800 s + 10 min = 1800 + 10*60 = 1800 + 600 = 2400 s,

x_i = 700 m, x = 0,

v₄ = a determinar;

luego, remplazas datos en la ecuación señalada (*), y queda:

0 = 700 + v₄*(2400 - 1800), resuelves el coeficiente en el último término, y queda:

0 = 700 + 600*v₄, restas 600*v₄ en ambos miembros, y queda:

-600*v₄ = 700, divides por -600 en ambos miembros, y queda: v₄ = -7/6 m/s;

luego, reemplazas el valor remarcado y los datos iniciales en la ecuación señalada (*), cancelas términos nulos, y queda:

x = 700 - (7/6)*(t - 1800) (en metros), con 1800 ≤ t ≤ 2400 (en segundos) (4).

Luego, con las expresiones e intervalos remarcados y señalados (1) (2) (3) (4) puedes plantear la expresión de la posición de María (expresada en metros) en función del tiempo (expresado en segundos):

x(t) = 

(2/3)*t                                         con      0 ≤ t ≤ 300

200                                              con   300 ≤ t ≤ 900

200 + (5/9)*(t - 900)                  con   900 ≤ t ≤ 1800

700 - (7/6)*(t - 1800)               , con 1800 ≤ t ≤ 2400

Luego, puedes reemplazar valores, y verás que los puntos extremos de tu gráfico, y los puntos de corte entre trozos son:

(0,0), (300,200), (900,200), (900,700) y (0,0);

luego, solo queda que hagas el gráfico cartesiano tiempo-posición.

Espero haberte ayudado.

Lo veo correcto :)

Debes corregir:

Tienes la expresión de la función:

f(x) = 2(x-1)(x+5), distribuyes el producto de agrupamientos, y queda:

f(x) = 2(x²+5x-1x-5), reduces términos semejantes en el agrupamiento, y queda:

f(x) = 2(x²+4x-5), distribuyes, y queda:

f(x) = 2x² + 8x - 10.

a)

Plantea la condición que cumplen los elementos del conjunto:

f(x) = 7, sustituyes la expresión desarrollada de la función que hemos remarcado, y queda:

2x² + 8x - 10 = 7, restas 7 en ambos miembros, y queda:

2x² + 8x - 17 = 0 (1), que es una ecuación polinómica cuadrática, la resuelves, y queda:

x₁ = ( -8+√(200) )/4 = ( -8+10√(2) )/4 = ( -4+5√(2) )/2 ≅ 1,5355,

x₂ = ( -8-√(200) )/4 = ( -8-10√(2) )/4 = ( -4-5√(2) )/2 ≅ -5,5355.

Luego, puedes continuar con la tarea.

Espero haberte ayudado.