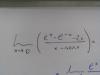-
Angel Garcia Curela
el 11/2/18 -
David Ru
el 11/2/18Hola , tengo una duda con un problema que me ha surgido en la vida real , tengo una pérgola la cual quiero cerrar con tablones de madera , la pergola mide de largo 4,3 metros , los tablones miden de largo 2,5 metros , la pergola mide de ancho 10 metros y los tablones 10 cm , de que forma tengo que cortar los tablones para hacer un uso lo más provechoso posible de los mismos , y cuántos de estos he de comprar ? , he estado pensando no se si se haría con una ecuación diofántica , o tratarla de otro modo , alguien podría decirme que modelo matemático usar
Ángel
el 12/2/18Pérgola----> 43dm x 100dm = 4300 dm2
Tablón-----> 25dm x 1dm= 25 dm2
Nº tablones en una pérgola= 4300 ÷ 25 = 172 tablones tienes que comprar
Cuando tengas 172 tablones, tendrás que proceder así:
*Sólo tienes que hacer cortes de 1 dm, "perfectamente" horizontales, todas las tablas usadas tienen 1dm de largo
1) 100 tablones los montas directamente sin cortar y cubres 2500 dm2
2) Los otros 72 tablones los cortas (divides) y sacas 72 piezas de 18 dm de largo y 72 piezas pequeñas de 7 dm de largo
3) Montas las 72 piezas de 18 dm2 junto los 100 tablones enteros y ya tienes cubiertos 2500+(18*72) = 2500+1296= 3796 dm2
4) Montas 56 piezas de las 72 piezas pequeñas de 7 dm de largo, dos en cada fila. (ya tienes cubiertos 4188 dm2 de los 4300 dm2)
5) Te quedan 16 piezas de 7 dm de largo y un hueco de 4 dm de largo y 28 dm de ancho
6) Cortas las 16 tablas obteniendo 16 de 4 dm de largo, las cuáles colocas y te quedan 16 tablillas de 3 dm y un hueco 4 dm de largo y 12 de ancho (cubiertos 4252 dm2)
7) Pones 12 tablillas de 3 dm de largo (te queda un hueco de 12 de ancho y uno de largo y 4 tablillas de 3dm2)
8) Cortas las 4 tablillas en 3 trozos de 1dm x 1 dm, obtienes 12 trozos y completas la pérgola.
En resumen: utilizas 100 tablones de 25dm de largo, 72 de 18dm, 56 de 7dm, , 16 de 4dm, 12 de 3 dm y 12 de 1dm
-
Adrian
el 11/2/18 -
Lsslie
el 11/2/18Buenas, me pueden ayudar con este ejercicio: Halla a, b y c en f(x) = x^3 + ax^2 + bx + c de modo que la gráfica de f(x) tenga tangente horizontal en x=1, su derivada en x=0 valga 1 y pase por el punto (1,-1). Graciaaas
-
M
el 11/2/18 -
Diego Schwindt
el 11/2/18 -
Adrian
el 11/2/18Buenos días, me pide 'proponer la ecuación del plano perpendicular a P:3x+4y+6z-12=0 que pase por el origen'
R:Ax+By×Cz+Z=0
p (0,0,0) como puedo seguir , se que el producto de los vectores normales tiene que ser igual a cero pero no llegó a nada.
-
Ashley
el 11/2/18
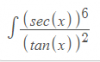
Buenas tardes, aqui esta el enunciado original .
