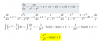-
Hola, he resuelto este problema de optimización pero tengo un problema, me de que en X=10 que es donde la 1a derivada =0 tiene un mínimo (2a derivada positiva). Y el ejercicio pide un máximo.
Gracias
Encontrad las longitudes de los catetos del triangulo rectángulo de área 50cm2 i hipotenusa mas grande posible. Comprobad que es, efectivamente, un máximo.
-
estoy trabajando con integrales tengo esta como ejercicio:
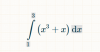
y al final despues de sustituir los limites inferiores y superiores en cada resultado de las integrales indefinidas , me terminan quedando los siguientes quebrados:
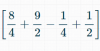
mi problema esta en que no manejo bien la parte de suma y resta de quebrados cuando los mismos pasan de 2, si alguien puede ayudarme lo agradeceria
-
Hola tengo dudas con este ejercicio me gustaria saber si se puede resolver esta ecuación usando usando solo los métodos vistos hasta nivel bachillerato. La verdad yo no he podido
La ecuación es:
2x =x2
Por inspección es claro que las soluciones son 2 y 4 pero no se si se pueda encontrar estos valores algebraicamente
-
Antonio Silvio Palmitano
el 14/12/17Vamos con una orientación.
a)
Considera la función cuya expresión es:
f(x) = x4 + 32x - 4, y observa que es continua en R;
luego, evalúa:
f(0) = 0 + 0 - 4 = -4 < 0,
f(1) = 1 + 32 - 4 = 29 > 0,
luego, aplicas el Teorema de Bolzano, y tienes que existe k ∈ [0,1] tal que:
f(k) = 0, luego, sustituyes la expresión de la función evaluada en el primer miembro, y queda:
k4 + 32k - 4 = 0.
b)
Considera la función cuya expresión es:
f(x) = x4 + 32x - 4, y observa que es continua en R;
luego, evalúa:
f(-4) = 256 - 128 - 4 = 124 > 0,
f(0) = 0 + 0 - 4 = -4 < 0,
luego, aplicas el Teorema de Bolzano, y tienes que existe m ∈ [-4,0] tal que:
f(m) = 0, luego, sustituyes la expresión de la función evaluada en el primer miembro, y queda:
m4 + 32m - 4 = 0.
c)
Considera la función cuya expresión es:
f(x) = x4 + 32x - 4, y observa que es continua en R;
luego, plantea la expresines de las funciones derivadas primera y segunda, y queda:
f ' (x) = 4x3 + 32 (observa que está definida en todo el dominio de la función),
f ' ' (x) = 12x2 (observa que está definida en todo el dominio de la función),
luego, plantea la condición de punto crítico (posible máximo o posible mínimo):
f ' (x) = 0, sustituyes, y queda:
4x3 + 32 = 0, divides por 4 en todos los términos de la ecuación, haces pasaje de término, y queda:
x3 = -8, haces pasaje de potencia como raíz, y queda:
x = -2;
luego, evalúas en la expresión de la derivada segunda, y queda:
f ' ' (-2) = 12(-2)2 = 48 > 0,
por lo que tienes que la gráfica de la función es cóncava hacia arriba en el punto crítico, y éste es un mínimo de la función,
y el valor de la función para él es:
f(-2) = (-2)4 + 32(-2) - 4 = 16 - 64 - 4 = -52 < 0.
Luego, debes completar el estudio de la gráfica de la función, y tienes:
que es decreciente y cóncava hacia arriba en el intervalo (-∞,-2),
y en x = -4, que pertenece a este intervalo, la función toma el valor f(-4) = 124 que es positivo;
alcanza un mínimo absoluto en x = -2, y para este valor la función toma el valor f(-2) = -52 que es negativo;
que es creciente y cóncava hacia arriba en el intervalo en el intervalo (-2,+∞),
y en x = 1, que pertenece a este intervalo, la función toma el valor f(1) = 27 que es positivo;
luego, puedes hacer un gráfico cualitativo, y verás que no existen otros puntos de intersección entre la gráfica de la función y el eje de abscisas OX, por lo que tienes que los únicos son k y m, de los que ya has demostrado su existencia, y son los únicos ceros de la función y, por lo tanto, son las únicas dos soluciones reales de la ecuación que tienes en el enunciado.
Espero haberte ayudado.
-
Una duda sobre Grafos: estoy buscando material que me explique como puedo averiguar con una matriz de adyacencia o con listas de adyacencia si un grafo es conexo, bipartito y si no es mucho pedir euleriano.En todo el material que he buscado no he encontrado una explicación.
Saludos
Antonius Benedictus
el 14/12/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).