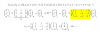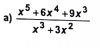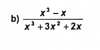-
Buenas tardes, David Calle:
¿cuando un alumno le pide un video, cuanto tarda en grabarlo y subirlo?Es que quiero que me suba un video de un ejercicio que no entiendo nada:
Selectividad 2017, Opción B, pregunta 2, apartado c
-
Antonio Silvio Palmitano
el 11/12/17Vamos por pasos
1°)
Considera la región limitada por las curvas cuyas ecuaciones son: y = x2 e y = 4,
y observa que sus vértices son los puntos: A(-2,4) y B(2,4), cuya área queda expresada:
A1 = ∫ (4 -x2)*dx = [ 4x - x3/3 ] = evalúas entre -2 y 2 = (8 - 8/3) - (-8 + 8/3) = 16/3 - (-16/3) = 32/3.
2°)
Considera la región limitada por las curvas cuyas ecuaciones son: y = x2 e y = c,
y observa que sus vértices son los puntos: C(-√(c),c) y D(√(c),c), cuya área queda expresada:
A2 = ∫ (c -x2)*dx = [ cx - x3/3 ] = evalúas entre -√(c) y √(c) = (c√(c) - (-√(c))3/3) - (-c√(c) + (√(c))3/3) = 2c√(c) - 2(√(c))3/3 =
= 2c√(c) - 2c√(c)/3 = 4c√(c)/3.
3°)
Luego, tienes la relación entre las áreas de las dos regiones:
A2 = (1/2)*A1, sustituyes expresiones, y queda:
4c√(c)/3 = (1/2)*(32/3), resuelves el segundo miembro, y queda:
4c√(c)/3 = 16/3, multiplicas en ambos miembros por 3/4, y queda:
c√(c) = 4, elevas al cuadrado en ambos miembros, y queda:
c2*c = 16, resuelves el producto de potencias con bases iguales, y queda:
c3 = 16, haces pasaje de potencia como raíz, y queda:
c = ∛(16).
Espero haberte ayudado.
-
√x4 + x2 + 9 ⁄ √x2+x+1 me pide el estudio complerto pero no puedo obtener la derivabilidad para ver los ceros de esa derivable
me pueden ayudar por favor
-
hola, una ayudita para este ejercicio por favor:
Dadas las rectas: r:x-1=y=-4z y s: (x,y,z)=(1,1,2)+h(1,2,0)
a) calcula la distancia entre r y s
b)calcula la ecuacion de la perpendiclar comun a r y sAntonius Benedictus
el 11/12/17 -
Buenas tardes, quería preguntaros a todos/AS si alguno de ustedes saben alguna página web o algún vídeo de unicoos sobre las progresiones y sucesiones de 3º ESO puesto que prácticamente no las entiendo. Muchas gracias.
Antonius Benedictus
el 11/12/17 -
Buenos días! Tengo algunas dificultades con dos problemas de álgebra, de 1r de carrera en ingeniería. Si alguien pudiera ayudarme lo agradecería mucho!
Gracias!!
Antonius Benedictus
el 11/12/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 11/12/171)
Tienes la integral:
I = 106*∫∫R x*dx*dy = pasas a coordenadas polares = 106*∫∫R r*cosθ*r*dr*dθ = 106*∫∫R r2*cosθ*dr*dθ, con los intervalos de integración:
0 ≤ r ≤ θ/(2π), 0 ≤ θ ≤ π/2.
Resuelves la integral para la variable r, y queda:
I = ( 106/(6π) ) * ∫ θ3*cosθ*dθ,
luego, planteas el Método de Integración por Partes:
u = θ3, de donde tienes: du = 3θ2*dθ,
dv = cosθ*dθ, de donde tienes v = senθ,
luego, aplicas el método y la integral queda:
I = ( 106/(6π) ) * ( θ3*senθ - 3*∫ θ2*senθ*dθ,
luego, debes aplicar el método nuevamente para resolver la integral secundaria (y si lo haces, observarás que deberás hacerlo dos veces más), hasta llegar a la expresión que debe evaluar entre 0 y π/2 (te dejo la tarea).
Espero haberte ayudado.
Antonio Silvio Palmitano
el 11/12/172)
Plantea el cambio a coordenada esféricas con eje OZ:
x = ρ*senφ*cosθ,
y = ρ*senφ*senθ,
z = ρ*cosφ,
cuyo factor de compensación (Jacobiano) es: |J| = ρ2*senφ;
con los intervalos de integración:
0,9 ≤ ρ ≤ 1,
0 ≤ φ ≤ π,
0 ≤ θ ≤ π,
luego, tienes la integral:
I = ∫∫∫B ( y/(x2+y2+z2) )*dx*dy*dz, haces el cambio de coordenadas, y queda:
I = ∫∫∫B (ρ*senφ*senθ/ρ2)*ρ2*senφ*dρ*dφ*dθ = simplificas = ∫∫∫B (ρ*sen2φ*senθ)*dρ*dφ*dθ,
luego, debes aplicar la identidad trigonométrica: sen2φ = (1/2)*( 1 - cos(2φ) ), para integrar con respecto a la variable φ,
y tienes que las integrales con respecto a la variable ρ y a la variable θ son directas (te dejo la tarea de hacer los cálculos).
Espero haberte ayudado.
-
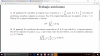
Hola de nuevo, le agradecería ayuda con este límite, no sé qué hacer a partir de la segunda indeterminación (no puedo utilizar L'Hôpital)
-
¡Buenos días! quizas usted me puedan ayudar con la fraccion de polinomios que le adjunto, me piden que simplifique, tengo el resultado pero no se que pasos seguir y como, gracias