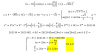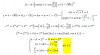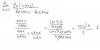
Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Mario Medina
el 10/12/17

hola buenas, no se como resolver este ejercicio, se que para obtener f(x) hay que integrar 2 veces y'':10x pero no se lo demas...

••0 voto/s
•
Antonius Benedictus
el 10/12/17

•1 voto/s
•
Neofito 007
el 10/12/17
La idea que tienes es prácticamente la única que se usa , sólo hay que ver como usar los datos .
Cuando integras la segunda derivada obtienes :
y ' = 5x^2 + C1
La recta tangente en ( 0 , 1) es horizontal , significa que la pendiente es 0 y sabes que esta se obtiene evaluando el punto en la primera derivada .Entonces :
m = 5(0^2) + C1 = 0 ==> C1 = 0
De donde :
y ' = 5x^2
Nuevamente integras y obtienes y
y = (5/3)x^3 + C2
El punto ( 0 , 1) pertenece a la curva , debe satisfacer su ecuación :
1 = (5/3)(0^3) + C2 ==> C2 = 1
Luego la función es :
f(x) = (5/3)x^3 + 1

•0 voto/s
•

Cancelar
Kt
el 10/12/17

Hola, buenas noches a todos, alguien me puede ayudar con este problema por favor? Explicar la parte de sacar las rectas a partir de que me digan "y las tangentes a esta con pendientes 4 y -4" por favor

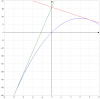
a)Calcula el area delimitada por la curva y=6x-x^2 y las tangentes a esta con pendientes "4" y "-4".
b)Representa la región delimitada.

••0 voto/s
•
Neofito 007
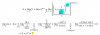
el 10/12/17
Cuestión de leer la teoría , la pendiente de la recta tangente en un punto P se calcula como la derivada de la función evaluado en dicho punto .
Sea el punto donde es tangente (x1 , y1) y (x2 , y2) ya que son 2 rectas , entonces :
y´(x1) = m1 = 4 .... en un caso
y´(x2) = m2= - 4 .... en otro caso
Ejemplo :
y´= 6 - 2x ==> 6 - 2(x1) = 4 ==> x1 = 1
Similar para el otro
Con ello encuentras x1 y x2 , si quieres obtener las ordenadas entonces sólo se evalúa en la función , dado que estos puntos pertenecen a la función.
y1 = y(x1)
y2 = y(x2)
Ejemplo :
y1 = y(x1) = y(1) = 6(1) - 1^2 = 5 , luego el punto es ( 1 , 5 ) y por allí pasa una recta de pendiente m = 4 tangente a la curva .

•1 voto/s
•

Cancelar
DIEGO
el 10/12/17

como se haria
(1/2)^-3: ( 1/2 )^-2

••0 voto/s
•
Ángel
el 10/12/17
(1/2)-3: ( 1/2 )-2 =
(1-3/2-3):( 1-2/2-2 ) =
(23/13):( 22/12 ) =
(8/1):( 4/1 ) =
8 : 4 =
2

•1 voto/s
•
Antonio
el 10/12/17
División de potencias de igual base: se restan los exponentes

(1/2)-3: ( 1/2 )-2 = (1/2)-3-(-2) = (1/2)-3+2 = (1/2)-1 = 2

•1 voto/s
•

Cancelar
Livaldo Ocanto
el 10/12/17

Si estoy en examen y tengo un sistema de ecuaciones de 3 incognitas con 3 ecuaciones o 4 incognitas con 4 ecuaciones (Ejemplo como quedan a veces las ecuaciones de kirchhoft), que metodo usarian rápido para resolver?

••0 voto/s
•
Antonius Benedictus
el 10/12/17
El método de Gauss, sin duda.

•0 voto/s
•

Cancelar
DIEGO
el 10/12/17

Me podrían ayudar a este ejercicio
( 0,002 )³x ( 6000 )⁴

••0 voto/s
•
Antonio
el 10/12/17
( 0,002 )3x ( 6000 )4 = ( 2/1000 )3x ( 6x1000 )4 =( 2³/1000³ ) x ( 6⁴x1000⁴ ) = 2³ x 6⁴x1000⁴/1000³=
= 2³ x 6⁴x1000 = 2³ x (2x3)⁴x1000 = 2³ x 2⁴x 3⁴x1000 = 2⁷ x 3⁴x1000

•1 voto/s
•
Ángel
el 10/12/17
( 0,002 )3 x ( 6000 )4 =
(2x10^-3)³x ( 6x10³)4 =
2³x10^-3x3 x 6⁴x10^3x4 =
2³x10^-9 x (2x3)⁴x10¹² =
2³x10^-9 x 2⁴x3⁴x10¹² =
2³⁺⁴x3⁴x10^-9+12 =
2⁷x3⁴x10³

•1 voto/s
•
Ángel
el 10/12/17
Es preferible dejar el resultado expresado en producto de factores primos:
( 0,002 )3 x ( 6000 )4 =
(2x10-3)3 x ( 6x103)4 =
23x10-3x3 x 64x103x4 =
23x10-9 x (2x3)4x1012 =
23x10-9 x 24x34x1012 =
23+4x34x10-9+12 =
27x34x103 =
27x34x(5x2)3 =
27x34x53x23 =
27+3x34x53 =
210x34x53

•1 voto/s
•

Cancelar
Sr.M
el 10/12/17

Ayuda por favor

••0 voto/s
•
Antonius Benedictus
el 10/12/17
Aquí lo tienes, con todos los pasos:
https://matrixcalc.org/es/#diagonalize%28%7B%7B3,2,-1%7D,%7B2,3,1%7D,%7B0,0,4%7D%7D%29

•1 voto/s
•
Sr.M
el 10/12/17
No conocía esa página para matrices. Muchas gracias !

•0 voto/s
•

Cancelar
Kt
el 10/12/17

Hola, buenas noches a todos, alguien me puede ayudar con este problema por favor?

a)Calcula el area delimitada por la curva y=6x-x^2 y las tangentes a esta con pendientes "4" y "-4".
b)Representa la región delimitada.

••0 voto/s
•
Antonio
el 10/12/17

•1 voto/s
•
Antonio
el 10/12/17
enlace

•1 voto/s
•
Kt
el 10/12/17
Entiendo como representas la curva que te dan, pero las dos rectas de donde las sacas? Donde sustituyes? No entiendo.

•1 voto/s
•
Kt
el 10/12/17
¿De donde sale la recta 14x + 16 y -2x+16? No sé como relacionar que las rectas sean tangentes y con pendientes -4 y 4

•1 voto/s
•
Antonio
el 10/12/17
mira este video

•0 voto/s
•

Cancelar
Javier García
el 10/12/17

Me pueden ayudar con estos limites? No me salen.

••0 voto/s
•
Livaldo Ocanto
el 10/12/17
Derivando

•0 voto/s
•
Antonius Benedictus
el 10/12/17

•2 voto/s
•
Antonius Benedictus
el 10/12/17

•2 voto/s
•

Cancelar
Francisco Fabrissin
el 10/12/17

Me ayudan por favor?!!
Para que valores de k los siguientes vecotores (5,-2,4);(k,-3,3);(3,1,9) forman el plano 2x+3y-z=0
Dar una base y dimencion para el mencionado plano.

Gracias!!!

••0 voto/s
•
Antonius Benedictus
el 10/12/17
2k-9-3=0
2k=12
k=6

•1 voto/s
•

Cancelar
Guido Ferrari
el 10/12/17

Me Ayudarian porfa?

••0 voto/s
•
Antonius Benedictus
el 10/12/17

•1 voto/s
•
Guido Ferrari
el 10/12/17
Una pregunta, por qué (4- (raiz de 48)i) lo elevó a la 6? Se simplifica o algo?

•0 voto/s
•
Antonius Benedictus
el 10/12/17
Lo he copiado mal. Ya te va correcto.

•1 voto/s
•
Antonius Benedictus
el 10/12/17

•1 voto/s
•

Cancelar