-
Fernando
el 9/12/17Ayuda con este ejercicio por favor.
a) Calcula que valor tendrá la K en la ecuación 3x + 7y + K= 0; para que P(-1, 4) pase por la recta.
b) Calcula el valor de K en la ecuación 8x - ky + 7= 0; para que la pendiente de la ecuación sea 2.
-
Erick Zambrana
el 9/12/17 -
Marta Losada
el 9/12/17 -
Sergio Rodríguez Moreno
el 9/12/17 -
carlos villalva
el 9/12/17
- Hola a todos , necesito ayuda con estos dos problemas de trigonometría sobre ángulos múltiples ( triple) ,gracias
Antonius Benedictus
el 9/12/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Ángel
el 9/12/17 - Hola a todos , necesito ayuda con estos dos problemas de trigonometría sobre ángulos múltiples ( triple) ,gracias
-
Jorge
el 9/12/17No sé hacer el ejercicio 2. b) (y por ende el c). ¡Ayuda!
-
Usuario eliminado
el 9/12/17
hola buenas, necesito ayuda con este ejercicio de integrales. gracias
-
Arturo
el 9/12/17Ayuda en problema de optimización?
Se divide un segmento de longitud 200 cm en dos trozos.Con uno de los trozos se forma un cuadrado y con el otro un rectangulo en el que la base es el doble de la altura.Calcula la longitud de cada trozo con la condición de que la suma de las áreas del cuadrado y del rectangulo sea mínima.
Gracias !
Antonio Silvio Palmitano
el 9/12/17Puedes designar con x a la longitud del lado del cuadrado, y la expresión de su área queda: A = x2,
y observa que la longitud de segmento empleada para formarlo es: LA = 4x.
Puedes llamar y a la longitud de la altura del rectángulo, y tienes que la longitud de su base es 2y, y la expresión de su área queda: B = 2y*y = 2y2,
y observa que la longitud de segmento empleada para formarlo es: LB = 2y + 2*2y = 2y + 4y = 6y.
Luego, tienes la longitud del segmento, por lo que puedes plantear:
4x + 6y = 200, divides por 4 en todos los términos de la ecuación, y queda:
x + (3/2)y = 50, haces pasaje de término, y queda:
x = 50 - (3/2)y (1).
Luego, plantea la expresión del área total:
AT = A + B, sustituyes expresiones, y queda:
AT = x2 + 2y2, sustituyes la expresión señalada (1), y tienes la expresión de la función:
AT(y) = (50 - (3/2)y)2 + 2y2, desarrollas el binomio elevado al cuadrado, y queda:
AT(y) = 2500 - 150y + (9/4)y2 + 2y2, reduces términos semejantes, ordenas términos, y queda:
AT(y) = (17/4)y2 - 150y + 2500, que es la expresión de la función a optimizar.
Luego, planteas la expresión de la función derivada, y queda:
AT ' (y) = (17/2)y - 150,
luego, planteas la condición de punto crítico (posible máximo o posible mínimo):
AT ' (y) = 0, sustituyes, y queda:
(17/2)y - 150 = 0, multiplicas en todos los términos de la ecuación por 2, y queda:
17y - 300 = 0, haces pasaje de término, y queda:
17y = 300, haces pasaje de factor como divisor, y queda:
y = 300/17;
luego, reemplazas en la ecuación señalada (1), y queda:
x = 50 - (3/2)(300/17) = 50 - 450/17 = 400/17.
Luego, tienes que la longitud del lado del cuadrado es: 400/17,
y tienes que la longitud de la base del rectángulo es: 600/17, y que la longitud de la altura del rectángulo es: 300/17.
Espero haberte ayudado.
-
Diego1705
el 8/12/17Hola queria saber cual es la primer y segunda derivada de esta funcion:
(x2-4)2/3
-
Augusto Alonso
el 8/12/17Me podrían ayudar a como resolver esta integral , Muchas Gracias
Integral (x^2 + 1)/(x^2 - 1)
Ángel
el 9/12/17Puedes hacer división de polinomios y expresar la fracción en forma de cociente+(resto/divisor), ya que ves que el cociente quedará como valor a integrar en uno de los sumandos y será 1 (y su integral equis)
∫(x2+1)/(x2-1) dx=
∫ 1+(2/(x2-1)) dx=
∫ 1 dx + ∫ 2/(x2-1) dx=
x + ∫ 2/(x2-1) dx=
x + ln|x-1|-ln|x+1|+C
**Intenta tú sacar la de ∫ 2/(x2-1) dx y si no te sale nos cuentas.
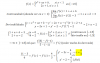
el problema 5 ya he logrado resolverlo pero me salió muy operativo tal vez haya otra forma de resolverlo ,el problema 6 solo he llegado hasta donde se ve en la imagen.
