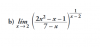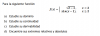-
x + y =1
ay + z= 0
x + (a+1)y + az = 1+a
Debo estudiarlo cuando a=0, debe ser por Cramer
Calculo el determinante de la matriz (sin result5ado) és 0, lo arreglo, quitando una, me sale determinante 1. Pero después en aplicar el método me salen zeros a los numeradores. Se perfectamente como se aplica, ya que he visto los videos.
César
el 7/12/17berni
el 9/12/17 -
La función f(x,y)=−(4x^2)/3−3y^2 en el punto (1, -1), cómo puedo saber en qué dirección tiene su máxima variación?
Antonio Silvio Palmitano
el 8/12/17Recuerda que la dirección de variación máxima de una función diferenciable en un punto, es la que corresponde al gradiente de la función evaluado en el punto.
Luego, observa que la función f es diferenciable en R2, por lo que planteas las expresiones de sus derivadas parciales, y quedan:
fx(x,y) = 8*x/3, evalúas para el punto en estudio, y tienes: fx(1,-1) = 8*1/3 = 8/3,
fy(x,y) = -6*y, evalúas para el punto en estudio, y tienes: fy(1,-1) = -6*(-1) = 6;
luego, planteas la expresión del vector gradiente evaluado en el punto en estudio, y queda:
∇f(1,-1) = < fx(1,-1) , fy(1,-1) > = < 8/3 , 6 >.
Espero haberte ayudado.
-
Lucas
el 7/12/17Muchas gracias profesor. Le comento la última duda del apartado d):
Cuando igualo a cero las funciones para determinar los extremos relativos, no obtengo en ninguna los puntos donde la derivada se anula. ¿Dónde estaré fallando?
- 1/2(2-x)^1/2 = 0
ln(x-1)+x/x-1 = 0
En ninguna obtengo solución.
Muchas gracias de nuevo,
Un saludo.
-
Antonio Silvio Palmitano
el 7/12/17Divides por 2 en todos los términos de la ecuación, y queda:
x4 + 2x3 - 2x2 - 3x + 2 = 0.
Observa que x = -2 es una solución de la ecuación, divides por (x+2) por medio de la Regla de Ruffini, y queda:
(x + 2)*(x3 - 2x + 1) = 0.
Observa que x = 1 es una solución del segundo factor, divides por (x-1) por medio de la Regla de Ruffini, y queda:
(x + 2)*(x - 1)*(x2 + x - 1) = 0.
Luego, por anulación de un producto, tienes tres opciones:
a)
x + 2 = 0, haces pasaje de término, y tienes la solución: x = -2;
b)
x - 1 = 0, haces pasaje de término, y tienes la solución: x = 1;
c)
x2 + x - 1 = 0,
que es una ecuación polinómica cuadrática cuyas dos soluciones son:
x = ( -1 - √(5) )/2 y x = ( -1 + √(5) )/2,
que son soluciones irracionales.
Por lo tanto, tienes que la ecuación del enunciado, que es de grado cuatro, presenta dos soluciones racionales (enteras) y dos soluciones irracionales.
Espero haberte ayudado.
-
Alguien puede ayudarme con este ejercicio de estadística?
En un test que evalúa el nivel de vocabulario, la media poblacional es 245 y la desviación típica 355. Esta variable, además, se distribuye normalmente. Teniendo en cuenta esa información contesta las siguientes preguntas.
- ¿Cuál es la puntuación correspondiente al percentil 90?
- ¿Qué percentil le correspondería a una persona que tuviera 255 puntos en ese test?
Sara Cuenca
el 7/12/17La tarea entera es esta, pero no se hacer el segundo ejercicio
EJERCICIO 1
- Calcula la correlación entre las variables “X” e “Y” y luego ponles nombre.
- Calcula la ecuación de regresión de Y sobre X.
- ¿Cuál es la puntuación estimada en la variable Y para un sujeto que tenga una puntuación de 14 en la variable X?
X
Y
6
11
5
9
7
16
8
13
EJERCICIO 2
En un test que evalúa el nivel de vocabulario, la media poblacional es 245 y la desviación típica 355. Esta variable, además, se distribuye normalmente. Teniendo en cuenta esa información contesta las siguientes preguntas.
- ¿Cuál es la puntuación correspondiente al percentil 90?
- ¿Qué percentil le correspondería a una persona que tuviera 255 puntos en ese test?
-
¿Alguien me puede ayudar con las siguientes series de fourier?
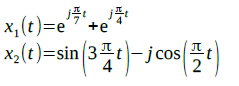
Gracias.
Antonius Benedictus
el 7/12/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).