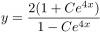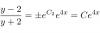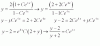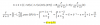-
Laura
el 4/12/17 -
Marest
el 4/12/17En un restaurant los comensales estaban sentados 8 en cada mesa, al notar que estaban muy juntos, se trajeron 6 mesas más y entonces ahora hay 5 en cada mesa. ¿Cuántos comensales hay?
Podrían ayudarme con este problema?
Muchas gracias.
-
David Ru
el 4/12/17
Por favor , alguien que me haga el desarrollo de como se pasa de una expresion a otra , no consigo hallar la manera , parto de la expresión de abajo y tengo que terminar en la de arriba , gracias
-
Marcos
el 4/12/17
Hola una duda..
En la regla de simpson compuesta cuando tengo que evaluar en la derivada cuarta, lo hago de la siguiente manera:
Grafico la derivada cuarta y en los valores a y b que me dan, y si a está mas arriba tomo a y evalúo a en la cuarta derivada, y si b es el que está mas arriba en el gráfico evalúo b en la cuarta derivada)
Es correcto?
Antonius Benedictus
el 4/12/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Héctor
el 4/12/17 -
Sergio Morantes
el 4/12/17ayudaaaa
hay que edificar un silo, (sin incluir la base) en forma de cilindro rematado por una semiesfera. el costo de la construccion por unidad cuadrada de superfice para la semiesfera es el doble del costo para la pared del cilindro. determina las dimensiones que han de usarse si el volumen es fijo y el costo de construccion ha de ser minimo. no consideres el espesor de la pared del silo ni el desperdicio generado durante la construccion.
-
Julio Rojas
el 4/12/17
buenas tengo un problema con este ejercicio me dice como sugerencia que lo haga con sustitucion x=tan pero lo intento y se que por fracciones parciales tambien sale pero quiero saber como hacerlo por sustitucion trigonometrica 
Antonio Silvio Palmitano
el 4/12/17Te ayudo con la integral.
Plantea la sustitución (cambio de variable):
x = tanw,
de donde tienes: dx = dw/cos2w,
también tienes: 1 + x2 = 1 + tan2w = 1/cos2w,
también tienes: x2 = tan2w = sen2w/cos2w,
y también tienes: arctanx = w (*).
Luego, plantea la expresión de la función que debes integrar:
x2/(1+x2)2 = sustituyes = (sen2w/cos2w) / (1/cos2w)2 = (sen2w/cos2w) / (1/cos4w) = sen2w*cos2w.
Luego, plantea la integral de tu enunciado:
I = ∫ ( x2 / (1+x2)2 )*dx = sustituyes = ∫ (sen2w*cos2w)*dw/cos2w = simplificas = ∫ sen2w*dw.
Luego, aplicas la identidad del cuadrado del seno de un ángulo en función del coseno de su doble, y queda:
I = ∫ (1/2)*( 1 - cos(2w) )*dw = resuelves = (1/2)*( w - (1/2)*sen(2w) ) + C = (1/2)*w - (1/4)*sen(2w) + C.
Luego, solo queda que sustituyas la expresión señalada (*).
Espero haberte ayudado.
-
SODA
el 4/12/17Tengo un problema con un ejercicio de rectas tangentes a la curva, derivación implícita. El enunciado es el siguiente:
Probar que no existen puntos sobre la gráfica x3+y3=3xy-1 en donde la recta tangente sea horizontal.
¡¡Ayuda!!
Antonio Silvio Palmitano
el 4/12/17Considera que la ecuación de la curva define a y como función de x, derivas implícitamente, y queda:
3x2 + 3y2*y ' = 3y + 3x*y ', divides por 3 en todos los términos de la ecuación, y queda:
x2 + y2*y ' = y + x*y ', haces pasajes de términos, y queda:
y2*y ' - x*y ' = y - x2, extraes factor común en el primer miembro, y queda:
(y2 - x)*y ' = y - x2, haces pasaje de factor como divisor, y queda:
y ' = (y - x2) / (y2 - x), y observa que debe cumplirse la condición: y2 - x ≠ 0 (*).
Luego, plantea la condición de recta tangente horizontal:
y ' = 0;
luego, reemplazas y queda la ecuación:
(y - x2) / (y2 - x) = 0, haces pasaje de divisor como factor, y queda:
y - x2 = 0, haces pasaje de término, y qeuda:
y = x2 (1),
que es la condición que deben cumplir las coordenadas del punto de contacto entre la curva y la recta tangente horizontal.
Luego, como el punto de contacto pertenece a la curva, sustituyes la expresión señalada (1) en la ecuación del enunciado, y queda:
x3 + (x2)3 = 3x(x2) - 1, resuelves términos, y queda:
x3 + x6 = 3x3 - 1, haces pasajes de términos, reduces términos semejantes, ordenas términos, y queda:
x6 - 2x3 + 1 = 0;
luego, aplica la sustitución (cambio de incógnita):
w = x3 (2),
luego sustituyes, y la ecuación queda:
w2 - 2w + 1 = 0, que es una ecuación polinómica cuadrática, cuya única solución es:
w = 1;
luego, reemplazas en la ecuación señalada (2), y queda:
1 = x3, haces pasaje de potencia como raíz, y queda:
1 = x, que es la abscisa que debe tener el punto de contacto entre la curva y la recta tangente horizontal;
luego, reemplazas en la ecuación señalada (1), y queda:
12 = y, resuelves y queda: 1 = y, que es la ordenada que debe tener el punto de contacto,
el que queda expresado, hasta este momento: A(1,1), cómo única posibilidas;
luego, observa que las coordenadas del punto A no cumplen con la condición señalada (*),
por lo que concluyes que no corresponde a una recta tangente horizontal y, como no tienes más posibles puntos, puedes concluir que la curva no presenta rectas tangentes horizontales.
Espero haberte ayudado.
-
Marco Tarazona
el 4/12/17please una ayudita con esta pregunta como saber si los vectores v=(2,-1,0) y w=(-3,4,6) son linealmente independientes en r3
Antonio Silvio Palmitano
el 4/12/17Plantea la "combinación lineal nula":
a*<2,-1,0> + b*<-3,4,6> = <0,0,0>, resuelves los productos externos en cada miembro, y queda
<2a-3b,-a+4b,6b> = <0,0,0>, luego igualas componente a componente, y queda el sistema de ecuaciones:
2a - 3b = 0
-a + 4b = 0
6b = 0, aquí haces pasaje de factor como divisor, y queda: b = 0;
luego, reemplazas en las demás ecuaciones, cancelas términos nulos, y queda:
2a = 0, aquí haces pasaje de factor como divisor, y queda: a = 0,
-a = 0, aquí multiplicas por -1 en ambos miembros, y también queda: a = 0.
Luego como los escalares a y b son ambos iguales a cero, tienes que los vectores son lineealmente independientes.
Espero haberte ayudado.
-
Arnau Tardío
el 4/12/17¿me podriais ayudar?
2. simplifica lo máximo q puedas.
(2x-3) · (3x+5)
