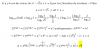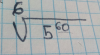-
Hola!! Me pueden ayudar con la siguiente ecuación trigonométrica:
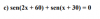
Desde ya muchas gracias, admiro su trabajo!!
Antonio Silvio Palmitano
el 6/12/17Recuerda la identidad de transformación en producto de a suma de dos senos:
senA + senB = 2*sen( (A+B)/2 )*cos( (A-B)/2 ),
y observa que en este ejercicio tienes:
A = 2x+60°, B = x+30°,
y luego tienes:
(A+B)/2 = ( 2x+60° + x+30° )/2 = (3x+90°)/2 = (3/2)x + 45°;
(A-B)/2 = ( 2x+60° - (x+30°) )/2 = (2x+60°-x-30°)/2 = (x+30°)/2 = (1/2)x + 15°.
Luego, plantea la ecuación del enunciado, aplicas la transformación, y queda:
2*sen( (3/2)x + 45° )*cos( (1/2)x + 15° ) = 0;
luego, haces pasaje de factor como divisor, y queda:
sen( (3/2)x + 45° )*cos( (x-30°)/2 ) = 0;
luego, por anulación de un producto, tienes dos opciones:
1)
sen( (3/2)x + 45° ) = 0, compones en ambos miembros con la función inversa del seno, y queda:
(3/2)x + 45° = 180°*k, con k ∈ Z,
haces pasaje de término en la ecuación, y queda.
(3/2)x = 180°*k - 45°,
multiplicas por 2/3 en todos los términos de a ecuación, y queda:
x =120°*k - 30°, con k ∈ Z;
2)
cos( (1/2)x + 15° ) = 0, compones en ambos miembros con la función inversa del coseno, y queda:
(1/2)x + 15° = 90° + 180°*m, con m ∈ Z,
haces pasaje de término en la ecuación, y queda.
(1/2)x = 75° + 180°*m,
multiplicas por 2 en todos los términos de a ecuación, y queda:
x =150°*k + 360°*m, con m ∈ Z.
Espero haberte ayudado.
-
Hola buenas tardes me podria ayudar con esta integral digo que es polares pero no puedo encontrar los limites de integracion y no se si ese x=y es lo mismo en polares como en cartesianas pero si me pueden ayudar con este ejercicio se los agradeceria mucho
La respuesta tiene que dar π
Antonio Silvio Palmitano
el 6/12/17Luego, observa que la región está limitada inferiormente por el eje OX (cuya ecuación es y = 0), y superiormente por la recta inclinada (cuya ecuación es y = x), por lo que tienes el intervalo de integración:
0 ≤ y ≤ x;
luego, observa que el punto qu está "más a la izquierda" en la región es el origen de coordenadas (cuya abscisa es x = 0), y que los puntos que están "más a la derecha" en la región pertenecen a la recta vertical (cuya ecuación es x = π), por lo que tienes el intervalo de integración:
0 ≤ x ≤ π.
Luego, pasamos a la resolución de la integral:
I = ∫∫R x*cosy*dy*dx = ∫ x * ( ∫ cosy*dy ) * dx;
resuelves la integral para y (observa que indicamos con corchetes que debemos evaluar con Regla de Barrow), y queda:
I = ∫ x * [ seny ] * dx = evaluamos = ∫ x * (senx - 0) * dx = ∫ x*senx*dx;
luego resuelves la integral para x con el Método de Integración por Partes (te dejo la tarea), y queda:
I = [ -x*cosx + senx ] = evaluamos = (-π*cosπ + senπ) - (0) = π.
Espero haberte ayudado.
-
Hola que tal tengo un ejercicio sobre CONICAS que no se si hice algo mal... Dejo una imagen de lo que realice desde ya gracias...
Ejercicio1: Determina la ecuacion canonica del lugar geometrico de los puntos del plano P(x,y) que cumpla las condiciones dadas en cada una de las siguientes situaciones:
c) Cuya diferencia de distancias a a F1= (1,4) y F2=(-1,4) es igual a 20.
-
Antonius Benedictus
el 5/12/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros
-
Ángel
el 5/12/176√(560) =
6√(56*56*56*56*56*56*56*56*56*56*) =
56/6*56/6*56/6*56/6*56/6*56/6*56/6*56/6*56/6*56/6=
51*51*51*51*51*51*51*51*51*51=
5*5*5*5*5*5*5*5*5*5=
510
o aplicando la propiedad 6√(560) = (560)1/6 = 560*(1/6) = 510
https://www.vitutor.com/di/re/b_3.html