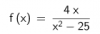-
Buenos días! Estoy con el tema de las ecuaciones y hay una que no logro entender cómo se resuelve. ¿Alguien podría explicarmela paso por paso, por favor? La ecuación es: x-5/3=2x-6/2
Ángel
el 5/12/17(x-5)/3 = (2x-6)/2
Pasamos a común denominador:
(2*(x-5))/6 = (3*(2x-6))/6
Multiplicamos por 6 a ambos lados de la ecuación para eliminar los denominadores:
2*(x-5) = 3*(2x-6)
Eliminamos los paréntesis multiplicando término a término:
2x-10 = 6x-18
Juntamos las x a un lado:
2x-6x = -18+10
Efectuamos las sumas/restas:
-4x = -8
Despejamos equis:
x= -8/(-4)
x= 2
-
Hola chicos(as) este ejercicio no lo entiendo muy bien es de integrales impropias es integral desde 1 a infinito positivo (1/8x-3 + 1/8x-1- 1/4x)dx Enserio me serviria de mucho ,ayudenme porfavor .Tengo examen mañana :)
Antonius Benedictus
el 5/12/17Ángel
el 5/12/17Para el examen de mañana (tienes poco tiempo) te recomiendo que vayas fijándote en como te las resuelve Symbolab https://es.symbolab.com/solver/definite-integral-calculator
y nos mandas un pantallazo señalando el paso que no entiendas (si lo hubiere) y te lo explicamos. Suerte.
-
he resuelto los ejercicios del a) a C) pero no pude resolver el problema d) ayuda por favor saludos, como se resolveria?
Antonius Benedictus
el 5/12/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Antonio Silvio Palmitano
el 5/12/17d)
Tienes el recinto de integración:
a ≤ x ≤ y (A),
a ≤ y ≤ b (B),
y para poder graficar, consideramos que a y b son estrictamente positivos, con a < b.
Luego, a partir del intervalo señalado (A) tienes las curvas, de las que señalamos sus ecuaciones cartesianas:
C1: x = a (recta paralela al eje OY, que pasa por el punto (a,0));
C2: x = y (recta bisectriz del primero, y del tercer cuadrante);
luego, haz un dibujo, observa que las curvas se cortan en el punto (a,a), y sombrea el sector limitado por la izquierda por la curva C1, y por la derecha por la curva C2.
Luego, a partir del intervalo señalado (B) tienes las curvas, de las que señalamos sus ecuaciones cartesianas:
D1: y = a (recta paralela al eje OX, que pasa por el punto (0,a));
D2: y = b (recta paralela al eje OX, que pasa por el punto (0,b));
luego, traza las dos rectas en el dibujo, y señala la porción del sector que ya has sombreado, limitado por debajo por la curva D1, y por arriba por la curva D2;
y observa que las curvas C1 y D1 se cortan en el punto (a,a), y que las curvas C2 y D2 se cortan en el punto (b,b).
Luego, observa que el sector señalado es un triángulo con vértices: (a,a), (a,b) y (b,b).
Luego, observa que el lado inferior del triángulo es un segmento de la recta de ecuación: y = x,
y que su lado superior es un segmento de la recta de ecuación: y = b,
por lo que tienes el intervalo:
x ≤ y ≤ b;
luego, observa que los puntos que se encuentran más a la izquierda del triángulo tienen abscisa: x = a,
y que el punto que se encuentra más a la derecha tiene abscisa: x = b,
por lo que tienes el intervalo:
a ≤ x ≤ b.
Luego, puedes plantear la integral en la forma (observa que indicamos con R a la región de integración, cuya representación gráfica es el triángulo señalado):
I = ∫∫R f(x,y)*dy*dx;
y como no tienes la expresión de la función, en este caso no es posible resolver la integral.
Espero haberte ayudado.
-
Francisco Bk Gtz
el 5/12/17Antonio Silvio Palmitano
el 5/12/17Puedes plantear la sustitución (cambio de variable):
xn = w, de donde tienes:
x2n = w2, y también tienes:
x-2n = 1/x2n = 1/w2,
y observa que w tiende a 1 cuando x tiende a 1.
Luego, sustituyes, y el límite queda:
Lím(w→1) (2w2 + 1 - 3/w2) / (3w2 - 5 + 2/w2) =
extraes factor común 1/w2 en el numerador y en el denominador, y queda:
= Lím(w→1) (1/w2)(2w4 + w2 - 3) / (1/w2)(3w4 - 5w2 + 2) =
simplificas, y queda:
= Lím(w→1) (2w4 + w2 - 3) / (3w4 - 5w2 + 2) =
aplicas la Regla de L'Hôpital (observa que también podrías factorizar por medio de la Regla de Ruffini, si prefieres), y queda:
= Lím(w→1) (8w3 + 2w) / (12w3 - 10w) =
resuelves, y queda:
= 10/2 = 5.
Espero haberte ayudado.
-
Hola, queria plantearles el siguiente ejercicio de probabilidades, a ver si me pueden ayudar:
Hay dos cajas, digamos la caja 1 y la caja 2:
Caja 1: Tiene el doble de pelotas azules que verdesCaja 2: Tiene el triple de pelotas azules que verdes
Caja 2: Tiene una pelota verde menos que la caja 1
Hay un total de 87 pelotas entre las dos cajas..
Como puedo calcular cuantas pelotas y de que colores son las que hay en la caja 1 y la caja 2?? Quisiera saber el procedimiento para calcularlo... No le encuentro la forma.. Gracias!
-
Hola. ¿Me podrian ayudar a resolver este ejercicio y también indicarme el nombre de las formas en las que están expresadas por favor?
Antonio Silvio Palmitano
el 5/12/17Vamos con una orientación.
Tienes el número complejo expresado en forma cartesiana binómica:
a = (1 - 2i)2 = desarrollas = 1 - 4i + 4i2 = 1 - 4i + 4(-1) = 1 - 4i - 4 = -3 - 4i.
Tienes el número complejo expresado en forma trigonométrica:
b = 4( cos(120°) + isen(120°) ) = reemplazas valores = 4( -1/2 + i√(3)/2 ) = distribuyes = -2 + 2√(3)i.
Tienes el número complejo expresado en forma trigonométrica:
c = 2e(π/3)i = expresas en forma trigonométrica = 2( cos(π/3) + isen(π/3) ) = reemplazas valores = 2( 1/2 + i√(3)/2 ) = distribuyes = 1 + √(3)i.
Luego, plantea la expresión del numerador:
a + b = -3 - 4i - 2 + 2√(3)i = -5 - ( 4 - 2√(3) )i.
Luego, plantea la expresión que tienes en el enunciado:
z = (a + b)/c = reemplazas:
= ( -5 - ( 4 - 2√(3) )i ) / ( 1 + √(3)i ) = multiplicas al numerador y al denominador por el conjugado del denominador:
= ( -5 - ( 4 - 2√(3) )i )( 1 - √(3)i ) / ( 1 + √(3)i )( 1 - √(3)i ) = y puedes continuar la tarea.
Espero haberte ayudado.
-
Esta integral ∫x^-2lnxdx se puede hacer por el metodo tabular??
Antonio Silvio Palmitano
el 5/12/17Observa que se puede resolver con el Método de Integración por partes:
u = lnx, de donde tienes: du = dx/x = x-1*dx;
dv = x-2*dx, de donde tienes: v = -x-1;
luego aplicas el método, y la integral queda:
I = -x-1*lnx - ∫ (-x-1)*(x-1)*dx = -x-1*lnx + ∫ x-2*dx = -x-1*lnx + (-x-1) + C = -x-1*lnx -x-1 + C.
Espero haberte ayudado.
JUAN AMPIE
el 5/12/17Ángel
el 5/12/17Creo que no es el método adecuado para esta integral, porque ni x-2 ni lnx se hacen cero alternando las derivadas o integrales sucesivas en uno u otro.
Por ejemplo puedes practicar con ∫(x3*ex)dx (observa que la cuarta derivada de x3 es cero, y a partir de ahí las sumas/restas son nulas)
-
Antonius Benedictus
el 5/12/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Antonio Silvio Palmitano
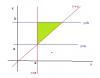
el 5/12/17Observa que el dominio de la función es: D = (-∞,-5) ∪ (-5,5) ∪ (5,+∞).
Luego, plantea la expresión de la función derivada primera:
f ' (x) = ( 4(x2-25) - 4x(2x) ) / (x2-25)2 = (4x2 - 100 - 8x2) / (x2-25)2 = (-4x2 - 100) / (x2-25)2 = - 4(x2+25) / (x2-25)2,
y observa que la función derivada primera está definida en todos los puntos del dominio de la función.
Luego, observa que la función derivada primera toma valores estrictamente negativos,
ya que su expresión es un producto entre un factor negativo (-4) y un factor positivo ( (x2+25) ),
y cuyo divisor es positivo ( (x2-25)2 );
por lo que tienes que la gráfica de la función es estrictamente decreciente en los dos subintervalos del dominio.
Espero haberte ayudado.
-
ayuda porfavor, creo que el siguiente punto da indeterminado pero no estoy seguro, porfavor ayudenme.
obtenga la ecuacion de la recta perpendicular a la tangente a la curva y=x^3 -3x en el punto de coordenadas (1,-2) y que pasa por el punto de coordenadas (3,1). dibuje la grafica de la curva e ilustre la situacion. obtenga la pendiente de la curva mediante la definicion de la derivada de una funcion: dy/dx= lim h→0 (f(x+h)-f(x))/h
Antonio Silvio Palmitano
el 5/12/17Plantea la expresión de la función derivada, a partir de la ecuación de la curva:
y ' = 3x2 - 3,
luego, evalúas para la abscisa del punto de contacto (x = 1), y tienes a pendiente de la recta tangente:
mT = 3(1)2 - 3 = 3 - 3 = 0,
por lo que tienes que la recta tangente es paralela al eje coordenado OX, y su ecuación cartesiana explícita es:
y = -2.
Luego, tienes que la recta perpendicular a la recta tangente es paralela al eje coordenado OY, y su ecuación cartesiana es:
x = 1.
Para el cálculo de la derivada de la función, comienza por plantear el incremento de la función:
f(x+h) - f(x) = ( (x+h)3 - 3(x+h) ) - (x3 - 3x) = desarrollas = x3 + 3x2h + 3xh2 + h3 - 3x - 3h - x3 + 3x = reduces términos semejantes (observa que tienes cancelaciones):
Espero haberte ayudado.
= 3x2h + 3xh2 + h3 - 3h = extraes factor común = h(3x2 + 3xh + h2 - 3);
luego, plantea el cociente incremental:
( f(x+h) - f(x) )/h = h(3x2 + 3xh + h2 - 3)/h = simplificas = 3x2 + 3xh + h2 - 3;
luego, plantea el límite del cociente incremental para el incremento (h) tendiendo a cero, y queda:
f ' (x) = Lím(h→0) ( f(x+h) - f(x) )/h = sustituyes = Lím(h→0) (3x2 + 3xh + h2 - 3) = resuelves = 3x2 - 3.
Espero haberte ayudado.
Sergio Morantes
el 5/12/17oye pero hago todo lo que me dijiste anteriormente pero cuando derivo por la definicion de limite me da 2, y se supone que tiene que dar 0 cuando derivo normalmente,
ademas de eso si hago la grafica de la pendiente de la recta tangente a la curva me da 0, y si tiene que dar 0, pero cuando voy a hallar la pendiente de la recta perpendicular a la recta tangente no me da, por que -1/0 da indeterminacion, entonces por eso pienso que es indeterminado, pero quisiera que lo comprobaras tu mismo para saber en que me equivoque.
gracias