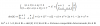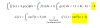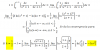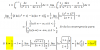-
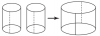
Cortamos 2 cilindros iguales por la línea punteada y se pegan juntos para formar un cilindro más grande (véase la figura). ¿Cuál es el resultado de dividir el volumen del cilindro grande entre el volumen de 1 de los cilindros pequeños?
-
hola me podrian ayudar con esta integral
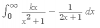 me pide hallar el valor de K en la cual converge segun el libro k =1/2 pero ni idea como hacerlo, gracias de antemano
me pide hallar el valor de K en la cual converge segun el libro k =1/2 pero ni idea como hacerlo, gracias de antemano Julio Rojas
el 5/12/17Antonio Silvio Palmitano
el 5/12/17Completamos.
Observa que el intervalo de integración es (0,+∞), y que la función a integrar es continua en todo el intervalo.
Recuerda la condición necesaria para la convergencia de la integral: el límite de la función a integrar debe ser cero para x tendiendo a +infinito.
Luego, observa que la expresión de la función puede escribirse
f(x) = kx/(x2+1) - 1/(2x+1) = extraes denominador común:
= ( kx(2x+1) - (x2+1) ) / (x2+1)(2x+1) = distribuyes en el numerador:
= (2kx2 + kx - x2 - 1) / (x2+1)(2x+1) = agrupas términos semejantes:
= ( (2k-1)x2 + kx - 1 ) / (x2+1)(2x+1).
Luego, plantea el límite para x tendiendo a +infinito de la función, y tienes dos opciones:
a)
2k - 1 ≠ 0, de donde tienes 2k ≠ 1, y luego tienes k ≠ 1/2:
Lím(x→+∞) ( (2k-1)x2 + kx - 1 ) / (x2+1)(2x+1) = (2k-1)/1 = 2k - 1 ≠ 0 (observa que el numerador y el denominador son expresiones polnómicas de grado 2);
b)
2k - 1 = 0, de donde tienes: 2k = 1, y luego tienes k = 1/2:
Lím(x→+∞) ( (2k-1)x2 + kx - 1 ) / (x2+1)(2x+1) = Lím(x→+∞) ( kx - 1 ) / (x2+1)(2x+1) = 0 (observa que el grado del numerador es menor que el grado del denominador).
Luego, tienes que en la opción (a) no se cumple la condición necesaria para la convergencia de la integral impropia,
y tienes que en la opción (b) si se cumple, por lo que debe cumplirse la condición: k = 1/2.
Luego, solo queda que reemplaces en la expresión de tu enunciado, y resuelvas la integral impropia a fin de determinar si es divergente o convergente.
Espero haberte ayudado.
-
Hola.
Si en el apartado c) de este ejercicio: https://www.youtube.com/watch?v=6cVczQWNtqk&index=1&list=PLOa7j0qx0jgOMGLQmkg9V2JnMOdpQsLp6
la raíz es negativa y David dice que eso quiere decir que la ecuación no tiene solución, pero no quiere decir que la inecuación no la tenga,
en este otro ejercicio: https://www.youtube.com/watch?v=eyC6Y4sjY_s&index=6&list=PLOa7j0qx0jgOMGLQmkg9V2JnMOdpQsLp6
¿Por qué sí descarta la solución negativa de la ecuación bicuadrada?
Gracias.
Un saludo.
César
el 5/12/17Ángel
el 5/12/17En el apartado c) del vídeo https://www.youtube.com/watch?v=6cVczQWNtqk&index=1&list=PLOa7j0qx0jgOMGLQmkg9V2JnMOdpQsLp6 :
Tenemos la inecuación 2x2-x+8 ≤ 0 (que incluye a los valores de equis que verifiquen 2x2-x+8 = 0 ó 2x2-x+8 < 0 )
1º) Como disponemos de una fórmula directa para estudiar 2x2-x+8 = 0 la usamos y obtenemos una raíz cuadrada negativa (por lo que no existen equis que verifiquen la ecuación)
2º) Al no obtener ninguna raíz sabemos que se cumplirá para TODO x que o bien 2x2-x+8 < 0 o bien 2x2-x+8 > 0
Entonces simplemente elegimos un valor al azar (David escogió el cero, tú puedes escoger el número que quieras entre -inf e inf) y obtienes que f(cualquier número) > 0 o lo que es lo mismo, es positivo
Como siempre será positivo y la inecuación "demanda" que sea negativo o cero, no se cumplirá en ningún caso y NO EXISTIRÁ SOLUCIÓN
-
Hola, necesito ayuda con estas integrales por cambio de variable:
a) (2x-1)/√(x+3)=
b)x∛(x-4)
Laura
el 5/12/17Antonio Silvio Palmitano
el 5/12/17b)
Puedes plantear la sustitución (cambio de variable):
x - 4 = w3, de donde tienes:
∛(x-4) = w, también tienes:
x = w3 + 4 (*), y también tienes:
dx = 3w2*dx.
Luego, tienes la integral:
I = ∫ x*∛(x-4)*dx = ∫ (w3 + 4)*∛(w3)*3w2*dw = 3*∫ (w3 + 4)*w*w2*dw,
luego, distribuyes en el argumento de la integral, y queda:
I = 3*∫ (w6 + 4w3)*dw;
luego, resuelves, y queda:
I = 3*(w7/7 + w4) + C = (3/7)*W7 + 3*W4 + C;
luego, sustituyes la expresión señalada (*), y queda:
I = (3/7)*( ∛(x-4) )7 + 3*( ∛(x-4) )4 + C = (3/7)*(x - 4)7/3 + 3*(x - 4)4/3 + C.
Espero haberte ayudado.
-
Hola necesito ayuda con esto:
un sistema de ecuaciones que se pueda resolver con el metodo (Newton raphson) y (gauss seidel). AYUDAAAAAAAAAAAAAAAAAAAAAAAAAAA :´(
Antonius Benedictus
el 5/12/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Ángel
el 5/12/17Seguramente te interesen los ej. del final y algún apartado del tema 3 para repasar: