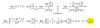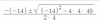-
Antonio Silvio Palmitano
el 24/10/17Puedes llamar y a la distancia entre el punto A y el punto B, y tienes que 9-y es la distancia entre el punto B y la refinería, y observa que las distancias se expresan en millas.
Luego, tienes los tramos de tubería:
*) subacuático, cuya longitud es x, y cuyo costo queda expresado: Ca(x) = 300000*x (1);
**) terrestre, cuya longitud es 9-y, y cuyo costo queda expresado: Cb(y) = 200000*(9 -y) (2).
Luego, observa el triángulo rectángulo que tienes en la figura, cuya hipotenusa tiene longitud x, su altura tiene longitud 4, y su base tiene longitud y, planteas la ecuación pitagórica, y queda:
42 + y2 = x2, resuelves el primer término, haces pasaje de término, y queda:
y2 = x2 - 16, haces pasaje de potencia como raíz, y queda:
y = √(x2 - 16) (3).
a)
Plantea la expresión del costo total:
C(x,y) = Ca(x) + Cb(y),
sustituyes las expresiones señaladas (1) (2), y queda:
C(x,y) = 300000*x + 200000*(9 -y),
distribuyes en el segundo término de la expresión, y queda:
C(x,y) = 300000*x + 1800000 - 200000*y,
sustituyes la expresión señalada (3), y queda la expresión del costo en función de una variable:
C(x) = 300000*x + 1800000 - 200000*√(x2 - 16).
Luego, plantea la expresión de la función derivada:
C ' (x) = 300000 - 200000*x/√(x2 - 16).
Luego, plantea la condición de punto crítico (posible máximo o posible mínimo):
300000 - 200000*x/√(x2 - 16) = 0,
divides por 100000 en todos los términos de la ecuación, y queda
3 - 2*x/√(x2 - 16) = 0, haces pasaje de término, y queda:
3 = 2*x/√(x2 - 16), elevas al cuadrado en ambos miembros, y queda:
9 = 4*x/(x2 - 16), haces pasaje de divisor como factor, y queda:
9*(x2 - 16) = 4*x, distribuyes en el primer término, y queda:
9*x2 - 144 = 4*x, haces pasaje de término, y queda:
9*x2 - 4*x - 144 = 0, que es una ecuación polinómica cuadrática, y tienes dos opciones:
1)
x = ( 4 - √(5200) )/18 ≅ -3,784, que no tiene sentido para este problema (recuerda que x es una longitud);
2)
x = ( 4 + √(5200) )/18 ≅ 4,228 millas, que si tiene sentido para este problema,
luego, reemplazas en la ecuación señalada (3), y queda:
y ≅ √(4,2282 - 16) ≅ 1,371 millas.
b)
Plantea que los costos quedan expresados:
*) subacuático, cuya longitud es 4 millas, y cuyo costo queda expresado: Ca(4) = 300000*4 = 1200000 (1);
**) terrestre, cuya longitud es 9 millas, y cuyo costo queda expresado: Cb(9) = 200000*9 = 1800000 (2).
Luego, sumas y tienes el costo total:
C = $ 3000000.
Espero haberte ayudado.
-
David
el 29/10/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Me podrían ayudar a hacer este ejercicio por medio de L'hopital
Se supone que da infinito
Gracias!
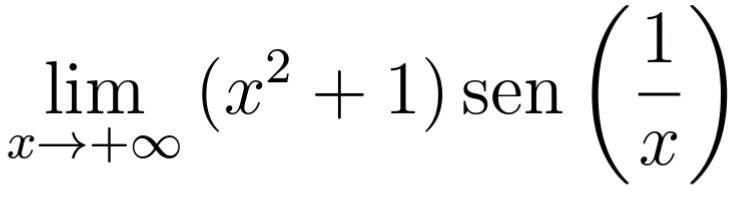
chado
el 24/10/17Moxie
el 24/10/17 -
Me podrían ayudar a hacer este ejercicio por favor?. Gracias.
7. Un alambre de longitud L es cortado en dos partes tal que uno de los partes tiene longitud x, es decir 0 ≤ x ≤ L . Con una de las partes e forma un círculo y con la otra, un cuadrado. Determine donde se debe cortar el alambre de manera que la suma de las áreas de las dos figuras sea
a) máxima.
b) mínima.
Antonio Silvio Palmitano
el 24/10/17Vamos con una orientación.
Puedes proponer que con la parte cuya longitud es x formas una circunferencia, por lo que tiene que su perímetro es x, por lo que puedes plantear:
2π*R = x, de donde despejas: R = x/(2π);
luego, plantea la expresión del área del círculo limitado por la circunferencia:
Ac = π*R2, luego, sustituyes la expresión del radio, y queda:
Ac = π*( x/(2π) )2, resuelves la potencia, simplificas, y queda:
Ac = ( 1/(4π) )*x2 (1).
Luego, tienes que con la parte cuya longitud es L-x formas un cuadrado, por lo que tienes que su perímetro es L-x, por lo que puedes plantear:
4*t = L-x, haces pasaje de factor como divisor, y la expresión del lado del cuadrado queda:
t = (L-x)/4;
luego, plantea la expresión del área limitada por el cuadrado:
At = t2, luego, sustituyes la expresión del lado, y queda:
At =( (L-x)/4 )2, resuelves la potencia, y queda:
At = (1/16)*(L - x)2 (2).
Luego, la expresión del área total queda:
A = Ac + At,
sustituyes las expresiones señaladas (1) (2), y tienes la función cuya variable es x:
A(x) = ( 1/(4π) )*x2 + (1/16)*(L - x)2,
luego, plantea la expresión de su derivada primera:
A ' (x) = ( 1/(2π) )*x - (1/8)*(L - x) (3),
luego, plantea la condición de punto crítico (posible máximo o posible mínimo:
A ' (x) = 0,
sustituyes la expresión señalada (3), y queda:
( 1/(2π) )*x - (1/8)*(L - x) = 0,
multiplicas en todos los términos de la ecuación por 8π, y queda:
4*x - π*(L - x) = 0,
distribuyes el segundo término, y queda:
4*x - π*L - π*x = 0,
haces pasaje de término, extraes factor común, y queda:
(4-π)*x = π*L,
haces pasaje de factor como divisor, y queda:
x = π*L/(4-π) ≅ 3,66*L.
Luego, tienes tres casos para evaluar:
x = 0 (formas solamente un cuadrado): A(0) = te dejo el cálculo;
x = π*L/(4-π) (formas un cuadrado y un círculo): A( π*L/(4-π) ) = te dejo el cálculo (que puedes realizar con el valor aproximado);
x = L (formas solamente un círculo): A(L) = te dejo el cálculo.
Luego, haz los tres cálculos y tendrás en uno de ellos el Máximo Absoluto, y en otro de ellos el Mínimo Absoluto.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 24/10/17Observa que tienes un sistema de tres ecuaciones lineales, con dos incógnitas.
Observa que la matriz del sistema (A) tiene tres filas y dos columnas, por lo que su rango es menor o igual que dos.
Observa que la matriz ampliada del sistema (A|B) tiene tres filas y tres columnas, por lo que su rango es menor o igual que tres.
Luego, haces pasaje de término en la última ecuación, y queda: y = -x (1),
luego, sustituyes la expresión señalada (1) en las dos primeras ecuaciones, extraes factores comunes, y queda:
(a-1)*x = -1
(a-2)*x = -b.
Luego, tienes las opciones:
1)
a = 1, reemplazas en la primera ecuación, y queda: 0 = -1, que es una identidad absurda, por lo que el sistema es incompatible y no tiene solución.
2)
a = 2, reemplazas, y el sistema queda:
x = -1, reemplazas en la ecuación señalada (1), y queda: y = 1,
0 = -b, aquí haces pasaje de término, y queda b = 0,
por lo que tienes que el sistema es compatible determinado y admite la solución única: x = -1, y = 1.
3)
a = 2 y b ≠ 0, reemplazas en la segunda ecuación, y queda: 0 = - b, que es una identidad absurda, por lo que el sistema es incompatible, y no tiene solución.
4)
a ≠ 2 y a ≠ 1, haces pasajes de factores como divisores en las dos ecuaciones, y queda:
x = -1/(a-1),
x = -b/(a-2),
luego igualas expresiones, y queda:
-b/(a-2) = -1/(a-1), multiplicas en ambos miembros por -1, haces pasaje de divisor como factor, y queda:
b = (a-2)/(a-1), y observa que si sustituyes en la segunda ecuación (que está sin remarcar), tienes que ésta coincide con la primera;
luego, sustituyes la primera expresión remarcada en la ecuación señalada (1), y queda: y = 1/(a-1),
por lo que tienes que el sistema es compatible determinado y admite la solución única: x = -1/(a-1), y = 1/(a-1).
Espero haberte ayudado.
-
Hola Unicoos. El ejercicio dice, estudiar la continuidad de esta función. Pero me he quedado atascada. Muchas gracias
Antonio Silvio Palmitano
el 24/10/17Obsrva que, una vez establecido el dominio (que has consignado correctamente), puedes "estandarizar" la expresión de la función, y para ello factorizas el numerador y el denominador, para luego simplificar:
f(x) = (x2 - 4) / (x2 - 2x), factorizas, y queda:
f(x) = (x+2)*(x-2) / ( x*(x-2) ), simplificas, y queda:
f(x) = (x + 2)/x.
Luego, estudia los límites de la función para cada punto de discontinuidad:
a)
Lím(x→0) f(x) = Lím(x→0) (x+2)/x = ±∞ (observa que el numerador tiende a 2, y que el denominador tiende a 0),
luego, estudias los límites laterales:
Lím(x→0-) f(x) = Lím(x→0-) (x+2)/x = -∞ (observa que el numerador tiende a 2, y que el denominador tiende a 0 desde valores negativos);
Lím(x→0+) f(x) = Lím(x→0+) (x+2)/x = +∞ (observa que el numerador tiende a 2, y que el denominador tiende a 0 desde valores positivos);
luego, tienes que la gráfica de la función presenta asíntota vertical, cuya ecuación es x = 0.
b)
Lím(x→2) f(x) = Lím(x→2) (x+2)/x = 2 (observa que el numerador tiende a 4, y que el denominador tiende a 2);
por lo que tienes que la gráfica de la función presenta discontinuidad puntual (o evitable) en x = 2.
Espero haberte ayudado.
-
Desencadenado
el 23/10/17Neofito 007
el 24/10/17Empiezo donde ya lo tienes hecho una buena parte .... simplemente continúo.
Acá hay un asunto muy importante cuando se divide por x , este x entra como x^2 al radical eso porque x es positivo y sqrt(x^2) = x , esa es la justificación .
Si el límite fuese por ejemplo cuando x tiene a menos infinito (acá x es negativo) y haces lo mismo de dividir por x .... etc . el resultado que se obtiene es incorrecto , tener cuidado allí . -
Hola, mi duda es con la derivada de la función de la imagen, ¿como la resolvería, como af o tendría que utilizar otra regla?
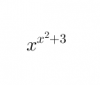
Neofito 007
el 23/10/17Una forma es emplear un método que se conoce como derivada logarítmica .
Otra forma alternativa que es prácticamente lo mismo que lo anterior es que mediante el uso de propiedades de los logaritmos trabajes la expresión y lo expreses de la forma
que ya conoces que es e^f , y allí aplicas la regla que conoces. Esta forma pongo en la imagen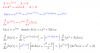
-
Ángel
el 23/10/17Ángel
el 24/10/17Si te piden hallar los valores de x en la ecuación 4x2-14x+49=0 tienes que seguir este proceso:
x1,2={-(-14)±√[(-14)2-4*4*49]}/(2*4)=
{+14±√(+196-784)}/8=
[14±√(-588)]/8=
{14±[√(588)*√(-1)]}/8=
[14±(√(588)*i)]/8=
[14±(√(72*3*22)*i)]/8=
[14±(7*2√(3)*i)]/8=
[14±(14i√3)]/8=
x1,2=[7±(7i√3)]/4
x1= [7+(7i√3)]/4
x2= [7-(7i√3)]/4