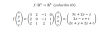-
Alvaro
el 18/10/17
necesito la derivada 62 y 63 . Ya sé que son un poco largas , agradecería muchísimo la ayuda
César
el 18/10/17https://es.symbolab.com/solver/derivative-calculator/%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft(%5Csqrt%7Bx%2B%5Csqrt%7Bx%2B%5Csqrt%7Bx%7D%7D%7D%5Cright)
https://es.symbolab.com/solver/derivative-calculator/%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft(ln%5Cleft(arctan%5Cfrac%7B1%2Bx%5E%7B2%7D%7D%7Bx%7D%5Cright)%5Cright)
-
Usuario eliminado
el 18/10/17Necessito la derivada de esto
( 2- t/200) x (24+3t) - (48 + 0,24t)
Ángel
el 18/10/17f´(x)= ( 2- t/200)´ * (24+3t) + ( 2- t/200) * (24+3t)´ - (48 + 0,24t)´
f´(x)= (0- 200/2002)*(24+3t) + (2- t/200)*(3) - (0+0,24)
f´(x)= (-1/200)*(24+3t) + (2- t/200)*(3) -0,24
f´(x)= -24/200- 3t/200 + 6 - 3t/200 -0,24
f´(x)= -24/200- 3t/200 + 1200/200 - 3t/200 -48/200
f´(x)= (-24-3t+1200-3t-48)/200
f´(x)= (1128-6t)/200
f´(x)= 1128/200 - 6t/200
f´(x)= 564/100 - 3t/100
f´(x)= (-3t+564)/100
-
Diego Mauricio Heredia
el 18/10/17
Saludos unicoos alguien seria amable en ayudarme con el inciso d?? Pasa que me estoy complicando un poco. 
Antonio Silvio Palmitano
el 18/10/17d)
Como tienes que la recta L es perpendicular a la recta L2, puedes considerar que su vector director es un vector perpendicular al vector director de la recta L2, (para obtenerlo rápidamente, permuta las componentes y cambia uno de sus signos), por ejemplo tienes:
u = <2,7> (vector director de la recta L)
A = <5,-3> (vector aplicado en el origen, cuyo extremo pertenece a la recta L);
luego, puedes plantear la ecuación vectorial paramétrica de la recta L2:
R = <5,-3> + ω*<2,7>, con ω ∈ ℛ.
Espero haberte ayudado.
-
ViRR
el 18/10/17Buenas tardes, estaba repasando matemáticas para un examen y me ha surgido la siguiente duda, ¿podrían ayudarme?:
Cuando quieres calcular la inversa de una matriz (por ejemplo de orden 3) o su rango con Gauss, al hacer ceros, por ejermplo, en la F2 , puedes hacer F3 - F2 o viceversa (F2 - F3), el resultado no va a cambiar.
En cambio, con los determinantes, el resultado sí cambia, y me gustaría saber cómo sé si, en este caso, tendría que restar F2 - F3 o restar F3 - F2 .
¡Muchísimas gracias!
-
Paloma fernandez
el 18/10/17
En que casos puedo multiplicar una fila de una matriz por un numero y multiplicar luego por la inversa la matriz?
Guillem De La Calle Vicente
el 18/10/17En el primer caso siempre: existen unas matrices que son casi la identidad salvo que el número por el que quieres multiplicar la fila j-ésima sustituye al 1 a la posición jj. Multiplica por esta matriz por la izquierda; si lo haces por la derecha se multiplicará la columna.
Y la segunda parte no se que quieres decir...
Saludos.
-
Sonia
el 18/10/17Hola, ¿podrían ayudarme con este problema? Gracias
El primer trimestre del curso pasado ocupó 8/25 de los días lectivos del curso completo. El segundo trimestre duró 13/35 del curso y el tercero 54 días. ¿Cuánto duró el curso completo? ¿Y cuánto duró cada trimestre?
Ángel
el 18/10/17El primer trimestre del curso pasado ocupó 8/25 de los días lectivos del curso completo= (8x)/25
El segundo trimestre duró 13/35 del curso= (13x)/35
y el tercero 54 días.
¿Cuánto duró el curso completo?
(8x)/25 + (13x)/35 + 54= x
(8x)/25 + (13x)/35 + 54/1= x/1
(56x+65x+9450)/175 = (175x)/175
(56x+65x+9450)
/175= (175x)/17556x+65x+9450 = 175x
9450 = 175x-56x-65x
9450 = 54x
x = 9450/54
x= 175 días duró el curso completo.
¿Y cuánto duró cada trimestre?
primer trimestre = (8x)/25
segundo trimestre = (13x)/35
tercer trimestre = 54 días duró el 3er trimestre. (dato del enunciado)
(8x)/25 = (8*175)/25 = 56 días duró el 1er trimestre.
(13x)/35 = (13*175)/35 = 65 días duró el 2º trimestre.
-
Héctor
el 18/10/17 -
Usuario eliminado
el 18/10/17 -
Jose I
el 18/10/17
Buenos días. ¿Alguien podria ayudarme coneste ejercicio y explicar como se hizo para saber si lo he entendido bien?
"Obtener las dimensiones de los espacios entre los que se define la aplicación 4.
Escriba las soluciones como un único valor numérico de 2 cifras, es decir si la aplicación fuera de r4 a r5 la solución sería 45, si fuera de r2 a r6 la solución sería 26, etc."Muchas gracias.
-
Alvaro González de Dios
el 18/10/17Hola, me podéis ayudar con este ejercicio? Gracias
Antonio Silvio Palmitano
el 18/10/17Tienes los sucesos:
M: "el paciente tomó medicamento";
L: "el paciente tomó placebo",
observa que los sucesos M y L son disjuntos;
C: "el paciente se curó".
Luego, tienes las probabilidades:
p(M) = 20/40 = 1/2 = 0,5,
p(L) = 20/40 = 1/2 = 0,5.
Luego, tienes las probabilidades condicionales:
p(C|M) = 0,85,
p(C|L) = 0,05.
a)
Plantea:
p(C) =
= p( (C∩M) ∪ (C∩L) ) =
= p(C∩M) + p(C∩L) =
= p(C|M)*p(M) + p(C|L)*p(L) =
= 0,85*0,5 + 0,05*0,5 = 0,425 + 0,025 = 0,45.
b)
p(M|C) =
= p(C∩M) / p(C) =
= p(C|M)*p(M) / p(C) =
= 0,85*0,5 / 0,45 = 0,425 / 0,45 ≅ 0,944.
Espero haberte ayudado.
