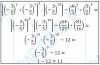Solo tienes que CONTAR:   6+6+4+4+6+1=27 posibilidades (para suma 9)

Sigue tú.

me puedes explicar que son las posibilidades reales ??

Contemos todas las opciones, como indica el colega Antonio Benito.

Para sacar nueve, tienes los siguientes casos:

126 162 216 261 612 621

135 153 315 351 513 531

144 414 441

225 252 522

234 243 324 342 423 432

333,

total: 25 casos.

Para sacar diez, tienes los siguientes casos:

136 163 316 361 613 631

145 154 415 451 514 541

226 262 622

235 253 325 352 523 532

244 424 442

334 343 433,

total: 27 casos.

Espero haberte ayudado.

Me disculpo: 

SUMA 9:   6+6+3+3+6+1=25 casos.

SUMA 10: 6+6+3+6+3+3=27 casos

Es muy restringido este Foro para explicarte dos semanas de Teoría de Conjuntos. Sube alguna duda concreta, muy concreta.

Entiendo el concepto de Relación, pero no soy capaz de ver cuando  es simétrico, antisimétrico, transitivo o reflexivo. Y, ¿qué es un conjunto cociente?. Con una buena definición me basta.

Muchas gracias

Diagramas de Venn

aqui tienes dos videos que te van a servir :D

Pon foto del enunciado original y te lo explicamos, Morgan.

No es lo mismo "menos" que "al menos"

Puedes llamar c a la cantidad total de cromos.

Luego, con el primer dato, puedes plantear que c es múltiplo de nueve:

c = 9x, donde x es la cantidad de cromos que hay en cada paquete.

Luego, con el segundo dato, puedes plantear que la cantidad de cromos excede en una unidad a un múltiplo de 11:

c = 11*y + 1, donde y es la cantidad de cromos que tiene cada uno de los once amigos, luego de ser repartidos.

Luego, con el tercer dato, puedes plantear que la cantidad total de cromos es menor que cinco docenas (5*12 = 60):

c < 60.

Luego, considera el primero y el tercer dato, y enumera los múltiplos de nueve que son menores que sesenta:

9, 18, 27, 36, 45, 54.

Luego, considera el segundo y el tercer dato, y enumera los números que exceden en una unidad a un múltiplo de once, que son menores que sesenta:

12, 23, 34, 45, 56.

Luego, observa que 45 es el número natural que cumple con las dos condiciones, por lo que tienes:

c = 45 cromos;

45 = 9*5, por lo que tienes cinco paquetes, con nueve cromos en cada paquete;

45 = 11*4 + 1, por lo que cada uno de los once amigos queda al final con cuatro cromos, y sobra uno.

Espero haberte ayudado.

Para que no haya dudas, ¿puedes poner foto del enunciado original?

gracias siento no haber respondido antes es que lo solucione

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

Plantea la ecuación diferencial homogénea asociada (observa que cambiamos la variable y por una nueva variable u):

2u ' + u = 0, haces pasaje de término, y queda:

2u ' = - u, expresas a la derivada como cociente entre diferenciales, y queda:

2du/dt = - u, separas variables, haces pasaje del factor numérico como divisor, y queda:

du/u = -(1/2)dt, integras y queda:

lnu = -(1/2)t (observa que omitimos la constante de integración en este paso), luego compones en ambos miembros con la función inversa del logaritmo natural, y queda:

u = e^-(1/2)t.

Luego, plantea la expresión de la solución general como el producto de la expresión remarcada por otra expresión a determinar:

y = w*e^-(1/2)t (1),

luego plantea la expresión de la función derivada:

y ' = w ' * e^-(1/2)t + w * e^-(1/2)t * (-1/2) = e^-(1/2)t * (w ' - (1/2)w,

luego sustituyes las dos expresiones en la ecuación diferencial del enunciado, y queda:

2( e^-(1/2)t * (w ' - (1/2)w ) + w*e^-(1/2)t = 4t,

distribuyes el primer término, y queda:

2*e^-(1/2)t * w ' - e^-(1/2)t * w + w*e^-(1/2)t = 4t,

cancelas términos opuestos, y queda:

2*e^-(1/2)t * w ' = 4t,

multiplicas en ambos miembros por (1/2)*e^(1/2)t, y queda:

w ' = 2t*e^(1/2)t,

expresas a la derivada como cociente entre diferenciales, y queda:

dw/dt = 2t*e^(1/2)t,

separas variables, y queda:

dw = 2t*e^(1/2)t*dt,

integras (observa que en el segundo miembro debes emplear el método de integración por partes), y queda:

w = 8*( (1/2)t - 1 )*e^(1/2)t + C (observa que en este paso si consignamos la constante de integración),

distribuyes los dos primeros factores, y queda:

w = (4t - 8)*e^(1/2)t + C,

luego, sustituyes en la expresión de la solución general señalada (1) y queda:

y = ( (4t - 8)*e^(1/2)t + C )*e^-(1/2)t,

luego distribuyes y la expresión de la solución general queda:

y = 4t - 8 + C*e^-(1/2)t (2),

luego, reemplaza los valores de la condición inicial que tienes en el enunciado (t = 0, y = 0), y queda:

0 = - 8 + C, haces pasaje de término, y queda:

8 = C,

luego reemplazas en la ecuación señalada (2) y queda:

y = 4t - 8 + 8*e^-(1/2)t,

que es la expresión de la solución particular de la ecuación diferencial sujeta a la condición inicial que tienes en el enunciado.

Espero haberte ayudado.

¿Puedes poner la foto? No sé qué es B con ?

Sean A y B dos sucesos de un experimento aleatorio. ¿Es posible que P sea una probabilidad si: P[A] = 2/5, P[B] = 1/5 y

P[A̅∩ (lo contrario de B)] = 3/10 ?

Observa que tienes dos casos:

1)

Si x > 0, la inecuación queda:

x² + 3x - 4 < 0, factorizas y queda:

(x + 4)(x-1) < 0, luego, por anulación de un producto tienes dos opciones:

a)

x + 4 > 0 y x - 1 < 0, haces pasajes de términos en ambas inecuaciones, y quedan: x > -4 y x < 1,

que corresponde al intervalo (0,1);

b)

x + 4 < 0 y x - 1 > 0, haces pasajes de términos en ambas inecuaciones, y quedan: x < -4 y x > 1,

que corresponde al intervalo vacío.

2)

Si x < 0, la inecuación queda:

x² + 3(-x) - 4 < 0, resuelves el signo en el segundo término, y queda:

x² - 3x - 4 < 0, factorizas y queda:

(x -4)(x+1) < 0, luego, por anulación de un producto tienes dos opciones:

a)

x - 4 > 0 y x + 1 < 0, haces pasajes de términos en ambas inecuaciones, y quedan: x > 4 y x < -1,

que corresponde al intervalo vacío;

b)

x - 4 < 0 y x + 1 > 0, haces pasajes de términos en ambas inecuaciones, y quedan: x < 4 y x > -1,

que corresponde al intervalo (-1,0).

Espero haberte ayudado.

126  admite  6 posibilidades (126, 162, 216, 261, 612, 621)

144   admite 3 posibilidades (144, 414, 441)

333  admite 1 posibilidad.

Ahora, haz el recuento completo de posibilidades REALES en cada uno de los sucesos ("Suma 9" y "Suma 10"), y verás.

hola antonio, gracias por ayudarme pero no lo entiendo, me lo podrías especificar ???

NO LO ENTIENDO ME LO PUEDES EXPLICAR PORFAVOR

En antecedentes:

hola antonio, creo que estoy peor que antes jejeje, me e liado mas .

¡Correcto!