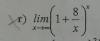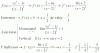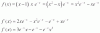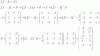-
chado
el 12/10/17tenes que usar limite para llevarlo a la forma del numero e
tenes que saber que
limte de x-->∞ (1+1/x )^x = e
por lo que en tu caso slo basta con trabajar el exponente
limte de x-->∞ (1+8/x )^8x/8
y como limte de x-->∞ (1+8/x )^x/8 .8 (la parte resaltada es =e
tu resultado es e^8
-
Hola necesito calcular crecimiento/decrecimientos y máximos y mínimos
x +1 / x2 - 1
Calculo asimptomas a -1 = -1/2, a 1 por la derecha +infinito, a 1 por la izquierda -infinito
hago derivada función pero el resultado para ver crecimiento salen los puntos que no estan el dominio
Antonio Silvio Palmitano
el 12/10/17Tienes la expresión de la función:
f(x) = (x + 1)/(x2-1) = (x + 1)/( (x+1)*(x-1) ) = 1/(x-1),
cuyo dominio es: D = R - { -1 , 1 } (observa que planteamos el dominio a partir de la expresión original de la función).
Luego, considera los límites:
Lím(x→-∞) f(x) = Lím(x→-∞) 1/(x-1) = 0 (observa que la expresión tiende a cero),
Lím(x→+∞) f(x) = Lím(x→+∞) 1/(x-1) = 0 (observa que la expresión tiende a cero),
por lo que tienes que la recta cuya ecuación es: y = 0 es asíntota horizontal por izquierda y por derecha);
Lím(x→-1) f(x) = Lím(x→-1) 1/(x-1) = 1/(-2) = -1/2,
por lo que tienes que la gráfica de la función presenta discontinuidad evitable (puntual) para x = -1;
Lím(x→1-) f(x) = Lím(x→1-) 1/(x-1) = -∞ (observa que el denominador tiende a cero desde valores negativos),
Lím(x→1+) f(x) = Lím(x→1+) 1/(x-1) = +∞ (observa que el denominador tiende a cero desde valores positivos),
por lo que tienes que la gráfica de la función presenta asíntota vertical, cuya ecuación es: x = 1.
Luego, plantea la expresión de la función derivada primera:
f ' (x) = -1/(x-1)2,
que está definida en todo el dominio de la función, (y observa que la expresión toma valores negativos en todo el dominio de la función), .
Luego, plantea la condición de punto crítico (posible máximo o posible mínimo):
f ' (x) = 0, sustituyes y queda:
-1/(x-1)2 = 0, haces pasaje de divisor como factor, y queda:
-1 = 0, que es una identidad absurda, por lo que tienes que la gráfica de la función no presenta puntos críticos (y observa que en tu desarrollo, en el cuál empleaste la expresión sin simplificar de la función, has obtenido los valores -1 y 1 que no pertenecen al dominio, por lo que tienes que la gráfica no presenta puntos críticos).
Luego, solo queda analizar en cada uno de los subintervalos del dominio cuáles son los signos de los valores que toma la función derivada primera, y como toma siempre valores negativos, tienes que la gráfica es decreciente en todos los subintervalos (es muy conveniente que recurras a un graficador para visualizar mejor la situación).
Espero haberte ayudado.
-
El ejercicio dice así: estudia la convergencia o la divergencia de esta serie de términos cualesquiera. Lo que más me interesa es saber el por qué de las cosas porque este ejercicio lo tengo resuelto y no lo entiendo. Muchas Gracias !!!!
-
Si f(x) una función de variable real
a)si f(x) es continua, es derivable
b) f (x) es derivable, es continua
c) f(x) no es derivable, no es continua
Ángel
el 11/10/17Antonio Silvio Palmitano
el 11/10/17Completamos.
a)
Considera la función valor absoluto:
f(x) = |x|, y observa que su dominio es R, observa que es continua en R, y en particular, es continua en x = 0, pero no es derivable en x = 0 (observa que su gráfica presenta un pico (punto anguloso) en x = 0).
b)
Te la ha contestado el colega Ángel.
c)
Otra vez, puedes recurrir a la función valor absoluto, observa que no es derivable en x = 0, pero si es continua en x = 0, y también a la función signo, que no es derivable en x = 0 y tampoco es continua en x = 0.
Espero haberte ayudado.
-
alguien sabe sacar un vector de módulo 2 de los vectores
B= 3i-k
C=5(i+j+k)
MGdR
el 11/10/17 -
Necesito la derivada de f(x) = (x-1) x e-x
Ángel
el 11/10/17 -
"Se lanza un dado dos veces. Calcula la probabilidad de que en la segunda tirada se obtenga un valor mayor que en la primera."
Alguien me puede ayudar con este ejercicio ??
Antonius Benedictus
el 11/10/17Antonius Benedictus
el 11/10/17Casos posibles:
Primera tirada 6. Por cada posible resultado, 6 posibles en la 2ª tirada. total: 6·6=36.
Casos a favor: si en la 1ª tirada sale un 1, en la segunda nos vale un 2, un 3, un 4 un 5 y un 6.
Si en la 1ª sale un 2, en la segunda nos vale un 3, un 4 un 5 y un 6.
Y así sucesivamente.