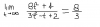con letras ; no será complejos?

Es la letra j no el numero complejo i. Ese es mi problema 

Observa que la función es diferenciable en R², pues es composición y producto de funciones diferenciables en R².

Luego, plantea las expresiones de sus derivadas parciales:

f_x(x,y) = e^x*sen(xy) + e^x*cos(xy)*y,

f_y(x,y) = e^x*cos(xy)*x.

Luego, plantea la expresión del diferencial total de la función:

df = f_x(x,y)*dx + f_y(x,y)*dy,

y solo queda que sustituyas las expresiones de las derivadas parciales.

Espero haberte ayudado.

Es decir cada vez que me piden calcular el diferencial de una funcion f(x,y) lo primero que hago es calcular las derivadas parciales para luego remplazar en la expresion del diferencial total ???

Osea en este caso entonces el diferencial de F(x,y)=e^x .sen (x.y) es :

df = [e^x (sen(xy)+cos(xy)] dx + [xe^x cos(xy)] dy   ???

Si, Lucas, es así.

Comienza por denominar:

x: cantidad de miembros del grupo A, y: cantidad de miembros del grupo B, z: cantidad de miembros del grupo C.

Luego, plantea las sumas recibidas por cada grupo: S_A = 20000x, S_B = 8000y, S_C = 10000z.

Luego, plantea la relación entre la suma recibida por el grupo A y la suma recibida por el grupo B: S_A = 5S_B.

Luego, tienes para la cantidad total de científicos:

x + y + z = 100 (1).

Luego, tienes para la distribución de los fondos recibidos:

S_A + S_B + S_C = 1360000, sustituyes expresiones, y queda:

20000x + 8000y + 10000z = 1360000, divides por 2000 en todos los términos de la ecuación, y queda:

10x + 4y + 5z = 680 (2).

Luego, tienes para la relación entre las sumas recibidas por los dos primeros grupos:

S_A = 5S_B, sustituyes expresiones, y queda:

20000x = 5(8000y), resuelves el segundo miembro, y queda:

20000x = 40000y, divides por 20000 en ambos miembros, y queda:

x = 2y (3).

Luego, sustituyes la expresión señalada (3) en las ecuaciones señaladas (1) (2), reduces términos semejantes, y queda el sistema:

3y + z = 100, aquí haces pasaje de término, y queda: z = 100 - 3y (4)

24y + 5z = 680;

luego sustituyes la expresión señalada (4) en la última ecuación, y queda:

24y + 5(100 - 3y) = 680,

distribuyes el segundo término, haces psaje de término, reduces términos semejantes, y queda:

9y = 180,

divides por 9 en ambos miembros de la ecuación, y queda: y = 20;

luego reemplazas el valor remarcado en la ecuación señalada (4), resuelves, y queda: z = 40;

luego reemplazas el primer valor remarcado en la ecuación señalada (3), resuelves, y queda: x = 40.

Espero haberte ayudado.

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

Vamos con el caso t tendiendo a +infinito, por lo que consideramos que t toma valores grandes y positivos, por lo que tienes también que t² toma valores mayores que t.

Plantea el valor absoluto de la diferencia entre el argumento del límite y su resultado:

|(8t²+4)/(3t²-t+2) - 8/3| =

extraes denominador común, resuelves el numerador (te dejo la tarea), y queda:

= |(8t-4) / ( 3(3t²-t+2) )| =

extraes factores comunes en el numerador y en el denominador, y queda:

= (4/3)|(2t-1) / (3t²-t+2)| ≤

sumas 1 en el numerador, restas 2 en el denominador (observa que el valor de la expresión aumenta), y queda:

≤ (4/3)|2t / (3t²-t)| =

extraes factor común en el denominador, y queda:

= (4/3)|2t / ( t(3t-1) )| =

simplificas, y queda:

= (4/3)|2/(3t-1)| <

sumas 1 y restas t en el denominador (observa que éste disminuye, por lo que la expresión aumenta), y queda:

< (4/3)|2/(2t)| =

simplificas y queda:

= (4/3)|1/t| = 

observa que el argumento del valor absoluto es positivo:

= (4/3)(1/t);

luego, observa que hemos probado la desigualdad:

|(8t²+4)/(3t²-t+2) - 8/3| < (4/3)(1/t).

Luego, planteamos la definición para el límite que tienes en el enunciado:

∀ ε > 0, ∃ k > 0 / t > k → |(8t²+4)/(3t²-t+2) - 8/3| < ε.

Para demostrar, planteamos el primer miembro de la última inecuación:

|(8t²+4)/(3t²-t+2) - 8/3| < 

observa la inecuación remarcada, la aplicas y queda:

< (4/3)(1/t) < ε;

haces pasajes de divisores como factores en la última inecuación remarcada, y queda:

4 < 3εt,

haces pasajes de factores como divisores, y queda

4/(3ε) < t,

escribes la inecuación tal cómo la lees de derecha a izquierda, y queda

t > 4/(3ε),

luego, puedes designar:

δ = 4/(3ε).

Espero haberte ayudado.

Que es lo que no te sale?

No consigo plantearlo como lo hace el profe Antonio, no se pruebo muchas cosas y no veo para solucionarlo y que me de la solución que me piden que es la misma de antonio. Este verano se nota que no hice nada...

Tienes que aprenderte las propiedades de los determinantes y, con paciencia y diligencia, usarlas adecuadamente.

Representa el costo básico (sin producción)

Sí, m=13 representa el costo por unidad y n=900 representa los "gastos fijos"

Fíjate en estos costes:

Fabricar 0 unidades:  13*0+900= 900 dólares

Fabricar 1 unidad:  13*1+900= 913 dólares

Fabricar 1000 unidades: 13*1000+900= 13900

Muchisimas gracias a los dos

Plantea la expresión de la función costo (que es lineal, según tu enunciado):

C(x) = m*x + b,

donde m y b son constantes cuyos valores debes determinar (observa que x expresa la cantidad de unidades fabricadas).

Luego, tienes que fabricar x = 100 (unidades) tiene un costo de 2200 (pesos diarios), 

luego reemplazas y tienes la ecuación:

2200 = 100*m + b, haces pasaje de término, y queda:

2200 - 100*m = b (1).

Luego, tienes que fabricar x = 300 (unidades) tiene un costo de 4800 (pesos diarios), 

luego reemplazas y tienes la ecuación:

4800 = 300*m + b, haces pasaje de término, y queda:

4800 - 300*m = b (2).

Luego, igualas las expresiones señaladas (1) (2) y queda la ecuación:

2200 - 100*m = 4800 - 300*m,

haces pasajes de términos, reduces términos semejantes, y queda:

200*m = 2600,

haces pasaje de factor como divisor, y queda: m = 13;

luego reemplazas el valor remarcado en las ecuaciones señaladas (1) (2) y queda (en ambas): 900 = b;

luego, reemplazas en la expresión de la función costo, y queda:

C(x) = 13*x + 900.

b)

La pendiente de la recta es 13 = 13/1, y representa el aumento del costo al fabricar un artículo adicional.

c)

La ordenada al origen es 900, y representa el costo inicial para poner todo en condiciones antes de comenzar a fabricar.

d)

Evalúas para x = 1000 (unidades), y queda:

C(1000) = 13*1000 + 900 = 13000 + 900 = 13900 (pesos diarios).

Espero haberte ayudado.

Tomando textualmente tu enunciado (observa que x tiende a cero por la derecha, ya que el logaritmo no está definido para valores menores o iguales que cero):

Observa que lnx tiende a -infinito, y, por lo tanto, el numerador tiende a +infinito.

Observa que el denominador tiende a -e.

Luego, tienes que el límite es -infinito, ya que que el numerador y el denominador tienen signos distintos.

Por otra parte.

Si x tiende a e, tienes el límite:

Lím(x→e) (1 - lnx)/(x - e) =

extraes factor común -1 y queda:

= - Lím(x→e) (lnx - 1)/(x - e) =

luego, observa que el límite corresponde a la expresión de la función derivada del logaritmo natural, evaluada para x = e (*), por lo tanto queda:

= - 1/e.

(*)

Plantea la definición de la derivada de la función: f(x) = lnx, evaluada en x = e (recuerda que has estudiado en clase que la expresión de la función derivada es: f ' (x) = 1/x, que evaluada queda: f ' (e) = 1/e):

f ' (e) = Lím(x→e) (lnx - lne)/(x - e) = Lím(x→e) (lnx - 1)/(x - e) = 1/e.

Espero haberte ayudado.

Establece un sistema de coordenadas con origen en el punto P, eje OX con sentido positivo hacia el punto S, y eje OY con sentido positivo hacia el punto Q.

Luego, plantea las coordenadas de los puntos según las especificaciones de tu enunciado (indicamos con 4p a la longitud del lado del cuadrado, por lo que p es un número real estrictamente positivo):

Puntos sobre el eje OX:

P(00), G(2p,0), S(4p,0),

y observa que el vector B queda:

B = PS = <4p-0,0-0> = <4p,0>.

Puntos sobre el eje OY:

P(0,0, Q(0,4p),

y observa que el vector A queda:

A = PQ = <0-0,4p-0> = <0,4p>.

Puntos sobre la recta paralela al eje OY

S(4p,0), F(4p,p), E(4p,2p), D(4p,3p), R(4p,4p).

Luego, plantea las ecuaciones cartesianas de las rectas:

L₁ (que pasa por los puntos G y D),

cuya pendiente es: m₁ = (3p-0)/(4p-2p) = 3p/(2p) = 3/2,

y cuya ecuación cartesiana explícita es: 

y = (3/2)x - 3p (1).

L₂ (que pasa por los puntos P y F):

cuya pendiente es: m₂ = (p-0)/(4p-0) = p/(4p) = 1/4,

y cuya ecuación cartesiana explícita es:

y = (1/4)x (2).

L₃ (que pasa por los puntos P y E):

cuya pendiente es: m₃ = (2p-0)/(4p-0) = 2p/(4p) = 1/2,

y cuya ecuación cartesiana explícita es:

y = (1/2)x (3).

Luego, puedes denominar con M al punto de aplicación del vector x, y observa que es el punto de intersección de las rectas L₁ y L₂, por lo que puedes plantear el sistema de ecuaciones:

y = (3/2)x - 3p

y = (1/4)x,

resuelves el sistema (te dejo la tarea) y tienes que las rectas se cortan en el punto M( 12p/5 , 3p/5 ).

Luego, puedes denominar con N al punto extremo del vector x, y observa que es el punto de intersección de las rectas L₁ y L₃, por lo que puedes plantear el sistema de ecuaciones:

y = (3/2)x - 3p

y = (1/2)x,

resuelves el sistema (te dejo la tarea) y tienes que las rectas se cortan en el punto N( 3p , 3p/2 ).

Luego, puedes plantear para el vector X:

x = MN = < 3p-12p/5 , 3p/2-3p/5 > = < 3p/5 , 9p/10 >;

luego, plantea la descomposición del vector según las direcciones de los ejes coordenados:

x = < 3p/5 , 0 > + < 0 , 9p/10 >,

multiplicas y divides por 4 en las componentes de los vectores, agrupas factores, y queda:

x = < 3(4p)/20 , 0 > + < 0 , 9(4p)/40 >,

extraes los factores numéricos no agrupados en ambos términos, y queda:

x = (3/20)*< 4p , 0 > + (9/40)*< 0 , 4p >,

sustituyes las expresiones remarcadas de los vectores A y B, y queda:

x = (3/20)*B + (9/40)*A,

que es la expresión del vector x en función de los vectores A y B.

Espero haberte ayudado.

Muchs gracias a los dos , me ha costado un poco verlo pero lo he entendido al final , gracias