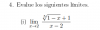Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Santiago
el 14/9/17

como resuelvo este limite?

••0 voto/s
•
Antonius Benedictus
el 14/9/17

•0 voto/s
•
Santiago
el 17/9/17
se puede hacer con la derivada de los limites?
es que aun no he visto l´Hopital entonces no la puedo usar

•0 voto/s
•

Cancelar
elkin eliecer moreno
el 14/9/17

Y el 18 como lo hago

••0 voto/s
•
Ángel
el 14/9/17

•1 voto/s
•

Cancelar
Alisson Ashanty Rojas Cruz
el 14/9/17

^{Buenas noches, disculpen podrían ayudarme con este ejercicio. He llegado a un punto en donde me he bloqueado y ya no se como resolverlo. (TT.TT) les agradecería mucho si me ayudaran.}
^{Por su atención gracias.}

••0 voto/s
•
Ángel
el 14/9/17

•0 voto/s
•
Ángel
el 14/9/17

•0 voto/s
•
Alisson Ashanty Rojas Cruz
el 14/9/17
Ángel, te vas a ir al cielo, muchas gracias!!!!!!!! :D

•2 voto/s
•

Cancelar
elkin eliecer moreno
el 14/9/17

Ayuda con el 16, No sé como hacerlo, gracias

••0 voto/s
•
Ángel
el 14/9/17

•1 voto/s
•

Cancelar
Santiago
el 14/9/17

ayuda con esto porfavor

••0 voto/s
•
Antonius Benedictus
el 14/9/17

•0 voto/s
•
Santiago
el 15/9/17
por que valores remplazas g(x) y f(x)?

•0 voto/s
•
Antonius Benedictus
el 15/9/17
Por los que se obtienen analizando las gráficas (tanto el valor de la ordenada como de la pendiente)

•0 voto/s
•

Cancelar
Aleatorius
el 14/9/17

Hola a todos, tiene algún nombre el hecho hacer el cambio sobre la línea de fracción; es decir, inicialmente se ve una fracción, pero luego se separa en dos fracciones sin alterar nada, como se llama ese paso?; se que no es "separa en términos".

••0 voto/s
•
Alvaro
el 14/9/17
No se si te refieres al hecho de simplificar , ya que realmente no creo que eso tenga nombre , ya que no es una operación en sí , no alteras nada. No sé si estoy en lo cierto.

•1 voto/s
•
Aleatorius
el 18/9/17
Gracias Alvaro por comentar, te cuento:
Es la propiedad conmutativa
Que dice que el orden de los factores no altera el producto entones, para verlo más fácil teniendo la fracción
a/b * a/b
Al multiplicar se multiplica arriba y abajo quedando
(a*a)/(b*b)
Por lo cual no importa cuál de las dos formas da el mismo resultado
(2*4)/(3*5)=2/3*4/5 ó 4/3*2/5

•0 voto/s
•

Cancelar
Desencadenado
el 14/9/17

Necesitaría la verificación de estos, en caso de que alguno tenga un resultado erróneo, la respuesta correcta.

••0 voto/s
•
Ángel
el 14/9/17

Te dice que al comienzo del mes (el día 1) hay 720 y te pregunta cuantos hay a final de mes (día 31); es decir: 30 días después
Entonces considero que hay 30 "incrementos" de 6 presos y un "decremento" de 150
Por lo que: 720+30*6-150 = 750

•1 voto/s
•
Desencadenado
el 14/9/17
Ángel fíjate que son dos imágenes.
Yo había tomado los 31 días como incremento.

•0 voto/s
•
Ángel
el 14/9/17
En la otra imagen lo veo todo perfecto.

•1 voto/s
•

Cancelar
Desencadenado
el 14/9/17

Podrían realizarme estos ejercicios por favor!

••0 voto/s
•
Ángel
el 14/9/17

•1 voto/s
•
Desencadenado
el 14/9/17
No se porque se me metió en la cabeza que eran números combinatorios, pero no me gustaban los resultados que obtenía.
Gracias Ángel!!!

•1 voto/s
•
Ángel
el 14/9/17
Si no te convencen los resultados que obtienes con la teoría, intenta razonarlo y puede que (no siempre) des con un método informal que te haga dar con el resultado de forma lógica y por lo tanto correcta
En el de los menús hay 12 combinaciones posibles (se ve perfectamente si te haces diagramas de árbol como el que te puse) y combinas:
Entrada(1), Plato(1),Postre(1)
Entrada(1), Plato(2),Postre(1)
Entrada(1), Plato(3),Postre(1)
Entrada(1), Plato(1),Postre(2)
Entrada(1), Plato(2),Postre(2)
Entrada(1), Plato(3),Postre(2)
Entrada(2), Plato(1),Postre(1)
Entrada(2), Plato(2),Postre(1)
Entrada(2), Plato(3),Postre(1)
Entrada(2), Plato(1),Postre(2)
Entrada(2), Plato(2),Postre(2)
Entrada(2), Plato(3),Postre(2)

En el otro, más de lo mismo.

Matemáticamente, el criterio o regla de multiplicación te salva de muchos apuros :D y todo esto que te dije lo puedes obviar...lo simplifica y mecaniza:
https://es.slideshare.net/TaniaAMonroy/regla-de-la-multiplicacin-y-permutacion

•0 voto/s
•

Cancelar
Santiago
el 14/9/17

Muy buenas unicoos.
Me podrían confirmar si esta bien este ejercicio de derivada implícita?
e^(y)*cos(x)=1+sin(xy)
dy/dx=(cos(xy) + e^y*sin(x))/(e^y*cos(x) - x)
muchas gracias.

••0 voto/s
•
Ángel
el 14/9/17
¿Puedes mandar foto del enunciado original con tu proceso/solución?

•0 voto/s
•
Santiago
el 14/9/17

•0 voto/s
•
Santiago
el 14/9/17

•0 voto/s
•
Ángel
el 14/9/17

•0 voto/s
•
Santiago
el 14/9/17
el xy´estaba a la derecha sumando, paso a la izquierda a restar
lo pase por que junté los terminos que tienen y´

•0 voto/s
•

Cancelar
Rj Mitte
el 13/9/17

Ayuda please

••0 voto/s
•
Alvaro
el 14/9/17
como el área de un triángulo es ( base x altura ) / 2 , y todos ellos tienen la misma altura y base, al menos es lo que se aprecia en la imagen , podemos decir que el área de todos ellos es [8 (base) x 4 (altura) ] / 2 = 16 . Podemos observar que todo triangulo con la misma base y altura tiene el mismo área , sin importar la forma.
Espero ayudar

•1 voto/s
•

Cancelar