-
JUAN AMPIE
el 12/9/17 -
Nico
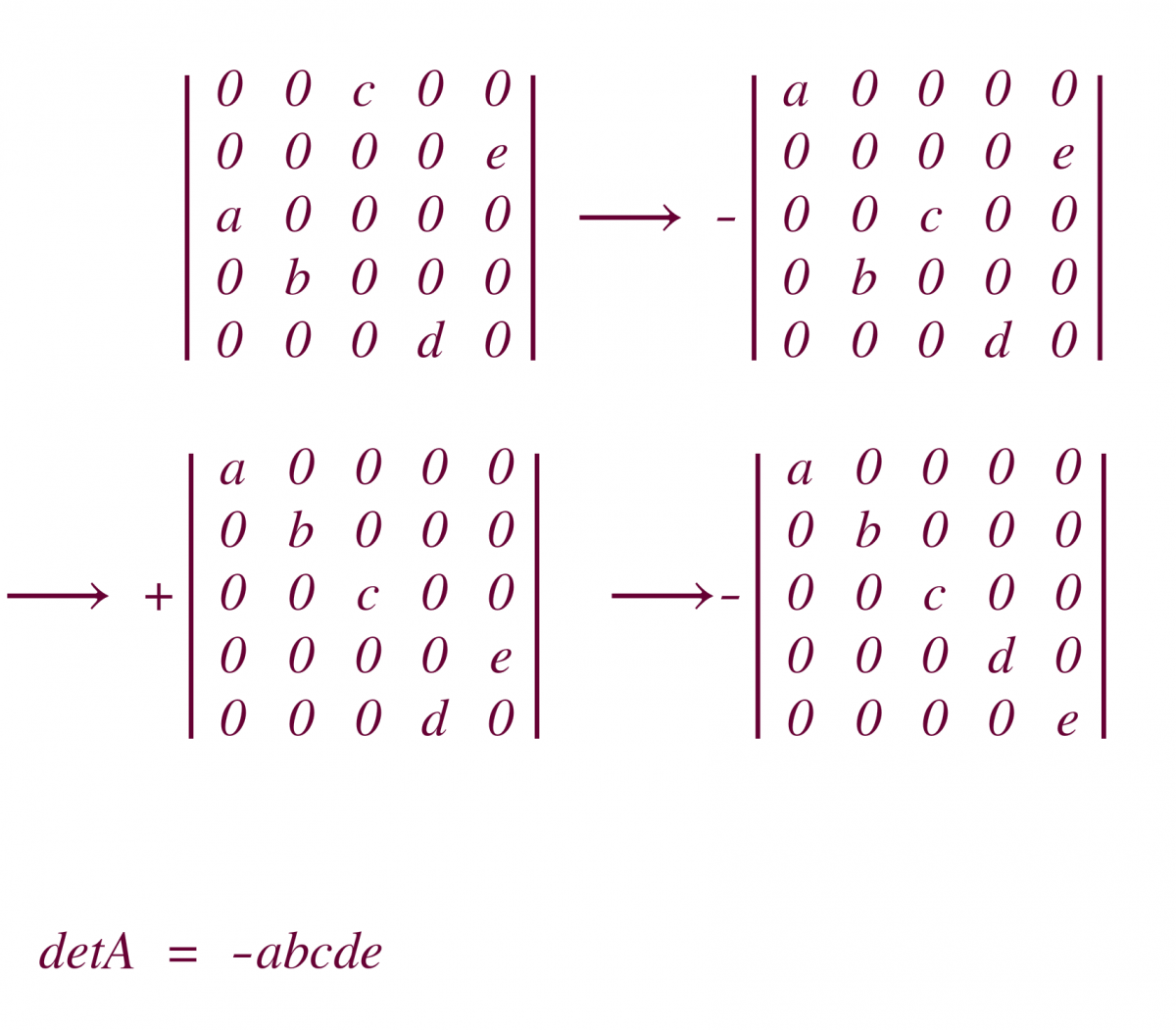
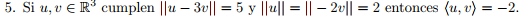el 12/9/17hola buenas noches, tengo una duda teórica, al derivar respecto de x me quedo la funcion 2/y -3y/x² y me piden especificar el dominio, mi duda es la siguiente: en la derivada respecto a x la y es una constante al derivar, pero despues que pasa con ella? sigue siendo constante o es variable? en ese caso no se que poner de dominio, porque si y=0 estoy jodido, el dominio se calcula respecto a x e y o solo respecto a x? disculpen tantas preguntas, es que tengo parcial :/
Antonio Silvio Palmitano
el 12/9/17Recuerda que el dominio de la función derivada debe estar incluid en el dominio de la función (observa que, a lo sumo, puede ser igual al dominio de la función).
Luego, una vez que has terminado el proceso de derivación, debes considerar que tienes una nueva función.
Si la expresión de la función original es:
f(x,y) = 2x/y + 3y/x,
tienes que su dominio es: A = R2 - {x=0} - {y=0}, cuya representación gráfica es el plano OXY sin los ejes coordenados OX y OY,
Luego, derivas parcialemente con respecto a x (y en el proceso consideras a y como constante, tal como señalas correctamente) y queda:
fx(x,y) = 2/y - 3y/x2,
que es una expresión de una nueva función de dos variables,
luego, tienes que su dominio coincide con el dominio de la función.
Espero haberte ayudado.
-
jovanna
el 12/9/17No sé cómo realizar la siguiente derivada:
y= tan ( 4x2 ) sen ( 5x )
dy/dx = tan ( 4x2 ) dy/dx sen ( 5x ) + sen ( 5x ) dy/dx tan (4x2 )
dy/dx = sec2 (4x2 ) cos ( 5x ) + cos ( 5x ) sec2 (4x2 )
Después de ahí, ¿cómo continuo?
jovanna
el 12/9/17
Desencadenado
el 12/9/17
Desencadenado
el 12/9/17 -
Nacho
el 12/9/17 -
Guillem De La Calle Vicente
el 12/9/17El conjugado de un número complejo z=u+iv (siendo u y v números reales) es el número complejo z'=u-iv. El conjugado de una suma (o producto) de dos números complejos es la suma (o producto) de los conjugados. Sabiendo que si z=u+iv es una raíz compleja de un polinomio P con coeficientes reales, entonces su conjugado z' es también una raíz de P. Demuestre que si z=u+iv (siendo u y v números reales) es una raíz compleja de un polinomio P con coeficientes reales, entonces P debe tener el factor cuadrático x2-2ux+u2+v2.
-
Juan R
el 11/9/17"Sean a y b dos números reales positivos. Si a+b y (a^2 - b^2) son números racionales, entonces:
a) a y b han de ser ambos racionales.
b) Existen a (perteneciente a los números racionales) y b (perteneciente a los irracionales) que verifican las condiciones del enunciado.
c) Existen a y b, ambos irracionales, que verifican las condiciones del enunciado.
d) No es cierta ninguna de las otras tres respuestas"
Se supone que la respuesta correcta es la a), ¿Alguien puede explicármelo? ¿Como me enfrento a este tipo de problemas? no sé cómo empezar.
-
Alejandro Torralba
el 11/9/17Buenas tardes, no sé como realizar este ejercicio:
-Expresa las razones trigonométricas del ángulo 285º con referencia a un ángulo del primer cuadrante
Me dice que las soluciones son: sen 285º= -cos 15º ; cos 285º= sen 15º ; tan 285º= -(1/tan 15º)
Si alguien pudiera aportar un dibujo para ayudarme a entenderlo lo agradecería :)
Antonio Silvio Palmitano
el 11/9/17Puedes emplear las identidades para la suma de dos ángulos, observa que puedes escribir: 285° = 270° + 15°,
y que tienes los valores: sen(270°) = - 1, y cos(270°) = 0.
1)
sen(285°) = sen(270°+15°) = sen(270°)*cos(15°) + cos(270°)*sen(15°) = -1*cos(15°) + 0*sen(15°) = -cos(15°) + 0 = - cos(15°).
2)
cos(285°) = cos(270°+15°) = cos(270°)*cos(15°) - sen(270°)*sen(15°) = 0*cos(15°) - (-1)*sen(15°) = 0 + sen(15°) = sen(15°).
Puedes emplear la identidad de la tangente en función del seno y del coseno.
3)
tan(285°) = sen(285°) / cos(285°) = - cos(15°) / sen(15°) = - 1 / ( sen(15°)/cos(15°) ) = - 1/tan(15°).
Espero haberte ayudado.
-
Deidara Stick.
el 11/9/17
Antonio Silvio Palmitano
el 11/9/17Recuerda las expresiones para los volúmenes de un cilindro circular recto (C), y de un cono circular recto (K), con diámemtro de su base d, y altura H:
VC = (π*D2/4)H (es el producto de la superficie de la base por la altura),
VK = (π*D2/4)*H/3 (es el producto de la superficie de la base, por la altura, dividido entre tres).
Luego, tienes para el cilindro (observa que el diámetro de su base es 4 u y que su altura es 10 u):
VC = π*42*10/4 = 40π u3.
Luego, tienes para el cono inferior (observa que el diámetro de su base es 4, y que llamamos y a su altura):
VKi = (π*42/4)y/3 = 4π*y/3.
Luego, tienes para el cono superior (observa que el diámetro de su base es 4, y que llamamos (10-y) a su altura):
VKs = (π*42/4)*(10-y)/3 = 4π*(10-y)/3 = distribuyes = 40π/3 - 4π*y/3.
Luego, plantea la suma de los volúmenes de los conos:
VKi + VKs = 4π*y/3 + 40π/3 - 4π*y/3 = 40π/3 u3.
Espero haberte ayudado.
-
Diego Mauricio Heredia
el 11/9/17 -
Deidara Stick.
el 11/9/17
Antonio Silvio Palmitano
el 11/9/17
Antonio Silvio Palmitano
el 11/9/17Comienza por plantear el desarrollo del binomio elevado a la séptima (observa que designamos con y al segundo término del binomio):
(x + y)7 = ∑(k=0;7) C(7,k)*x7-k*yk,
luego, observa que el término general es (observa que sustituimos la expresión del segundo término del binomio):
Tk = C(7,k)*x7-k*( 1/(a*x2 )k = C(7,k)*x7-k/(ak*x2k), aplicas la propiedad de la división de potencias con bases iguales y queda:
Tk = C(7,k)*x7-k-2k/ak, ordenas factores y reduces el exponente y queda:
Tk = ( C(7,k)/ak )*x7-3k;
luego, observa que para el término de grado 1 corresponde plantear para el exponente remarcado:
7 - 3k = 1, haces pasaje de término y queda: - 3k = - 6, haces pasaje de factor como divisor y queda: k = 2;
luego, reemplazas en la expresión del término general y queda:
T2 = ( C(7,2)/a2 )*x7-3(2), resuelves el exponente y queda:
T2 = ( C(7,2)/a2 )*x1,
luego, plantea para el coeficiente de este término, de acuerdo con tu enunciado:
C(7,2)/a2 = 7/3, resuelves el número combinatorio y queda:
21/a2 = 7/3, haces pasajes de divisores como factores y queda:
63 = 7a2, haces pasaje de factor como divisor y queda:
9 = a2, haces pasaje de potencia como raíz (observa que el exponente es par) y queda:
|3| = a.
Espero haberte ayudado.
