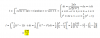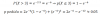-
Deidara Stick.
el 11/9/17x fa en unas horas tengo ese examen....
Que nervios... ayudame x favor
SAludos y muchas gracias
Antonio Silvio Palmitano
el 11/9/171)
Observa que tienes cinco dígitos, de los que debes elegir dos, sin repetición y con orden para formar un número de dos cifras distintas,
por lo que tienes Variaciones sin repetición de cinco elementos tomados de a dos:
V(5,2) = 5! / (5-2)! = 5! / 3! = 5*4*3! / 3! = 5*4 = 20 números.
Puedes verificar que los números son:
12 13 14 15 - 21 23 24 25 - 31 32 34 35 - 41 42 43 45 - 51 52 53 54.
2)
Puedes emplear el principio de multiplicación:
1°)
Elige el conductor:
tienes tres personas y debes elegir una:
N1 = 3 posibilidades.
2°)
Elige el acompañante en el asiento delantero:
tienes cuatro personas (observa que ya has elegido al conductor) y debes elegir una:
N2 = 4 posibilidades.
3°)
Ordenas a los pasajeros en el asiento trasero:
tienes tres personas (observa que ya has elegido al conductor y al acompañante), y los debes ordenar:
N3 = P(3) = 3! = 6 posibilidades.
Luego, por el principio de multiplicación tienes (observa que por cada uno de los tres posibles conductores tienes cuatro posibles acompañantes, y por cada elección de conductor y acompañante tienes seis formas de ubicar a los tres pasajeros en el asiento trasero):
N = N1*N2*N3 = 3*4*6 = 72 maneras.
Espero haberte ayudado.
-
Diego Mauricio Heredia
el 11/9/17
Alguien me podria decir con que formula o como hayo la altura h de un triangulo escaleno ????
-
Jesus Becerra
el 11/9/17tengo un problema, estoy calculando la matriz de transformación homogénea, y en ella me pide el vector posición, ya tengo los vectores unitarios de la nueva posición, pero me falta la nueva posición de origen, alguien que me colabore para hallar el punto donde se interceptan los vectores unitarios, supongo que esa seria la cuestión, ya que donde se intercepten los tres vectores debería ser el origen del nuevo plano 3D
Antonius Benedictus
el 11/9/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Luis Miguel Villacis
el 11/9/17 -
Juan
el 11/9/17Buenas! Querias saber si estaba bien este ejercicio de integrales.. lo hice de esta manera pero no estoy muy convencido :$
Luis Miguel Villacis
el 11/9/17u=√(2x+1) ---> despejando x=(u2-1)/2
du=(2/2√(2x+1)) dx
du=(1/u)dx ---> despejando dx=udu
Reemplazando en la función respectivamente....
∫((u2-1)/2)(u)(u) du
resolviendo la operación nos queda
∫(u4-u2)/2 du
seperando las integrales
∫u4/2 du - ∫u2/2 du
Integrando
u5/10-u3/6
regresando a todos en términos de "x"
(√(2x+1))5/10 - (√(2x+1))3/6
Evaluando los límites
((√(2(4)+1))5/10 - (√(2(4)+1))3/6) - ((√(2(0)+1))5/10 - (√2(0)+1))3/6)
((√(9))5/10 - (√(9))3/6) - ((√(0+1))5/10 - (√(0+1))3/6)
35/10 - 33/6 - 1/10 + 1/6298/15
-
Cristian Alvarez
el 11/9/17Buenas tengo este ejercicio e intente resolverlo por la formula general de la recta y tmb por la pendiente pero no puedo no logro resolverlo alguien me puede ayudar porfavor: me pide hallar la ecuacion de la recta
Situada 5 unidades por debajo del eje x su solucion es y+5=0
Ángel
el 11/9/17y=mx+n
m=pendiente= "lo que aumenta la y entre lo que aumenta la x" -------------> La y se mantiene constante, no aumenta, por lo que el aumento siempre es cero ----> 0/k = 0
n= ordenada en el origen -----> (0, -5) = (0,y) -------> n= -5
Entonces la ecuación de la recta y=mx+n pasa a ser y=0*x+(-5) --------> y= -5 -----> y+5=0
-
Santiago
el 11/9/17 -
Guillem De La Calle Vicente
el 11/9/17 -
Guillem De La Calle Vicente
el 11/9/17El conjugado de un número complejo z=u+iv (siendo u y v números reales) es el número complejo z'=u-iv. El conjugado de una suma (o producto) de dos números complejos es la suma (o producto) de los conjugados. Utilice este hecho para verificar que si z=u+iv es una raíz compleja de un polinomio P con coeficientes reales, entonces su conjugado z' es también una raíz de P.
-
Santiago Gamboa
el 11/9/17hola unicoos ayuda con esto: Para que valores de x la función f(x) = |x^2 - 9| es derivable y cual es su derivada
Ángel
el 11/9/17Se define la función a trozos:
f(x) = x^2 - 9 si x≤ -3
-x^2 + 9 si -3 < x ≤ 3
x^2 - 9 si x > 3
Y su derivada:
f´(x)= 2x si x< -3
-2x si -3 < x < 3
2x si x > 3
Verificas antes de todo que f(x) es contínua en todo R
Posibles puntos de no derivabilidad
lim (x-> -3-) f(x) = 2*(-3)= -6
lim (x-> -3+) f(x) = -2*(-3)= +6
Como no coinciden, no es derivable en x= -3
lim (x-> 3-) f(x) = -2*(3)= -6
lim (x-> 3+) f(x) = 2*(3)= +6
Como no coinciden, no es derivable en x= 3ES DERIVABLE EN TODO ℛ MENOS x= -3 y x= 3
Santiago Gamboa
el 11/9/17
Ángel
el 11/9/17Estudiamos donde habrá un cambio de signo. Para ello igualamos a cero:
x^2-9=0 -------> x^2=9 -----> x= -3 , x= 3
Obtenemos los siguientes intervalos:
(-inf,-3)
(-3,3)
(3,inf)
Damos un valor aleatorio en cada intervalo:
(-inf,-3) --------> Damos el valor -5 a x en x^2-9 y obtenemos (-5)^2 -9 = 16 ------> POSITIVO (no cambia la función dentro del v.absol. -----> x^2-9
(-3,3) --------> Damos el valor 0 a x en x^2-9 y obtenemos (0)^2 -9 = -9 ------> NEGATIVO (cambia) -----> -(x^2-9) = -x^2+9
(3,inf) --------> Damos el valor 5 a x en x^2-9 y obtenemos (5)^2 -9 = 16 ------> POSITIVO (no cambia) -----> x^2-9
