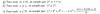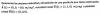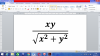
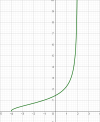
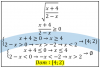
Observa que el dominio de la función es: D = R² - {(0,0)}.

Luego, puedes plantear el cambio a coordenadas polares (x = r*cosθ, y = r*senθ),

luego sustituyes y la expresión de la función queda:

f(r,θ) = r²*cosθ*senθ / √( r²*(cos²θ+sen₂θ) ) = r²*cosθ*senθ / √( r²*1 ) = r²*cosθ*senθ / r = r*cosθ*senθ;

luego aplicas la identidad trigonométrica: cosθ*senθ = sen(2θ)/2 en el numerador, y la expresión de la función queda:

f(r,θ) = r*sen(2θ)/2 = (r/2)*sen(2θ).

Luego, observa que el primer factor toma valores positivos (recuerda que la variable polar r toma valores positivos) distintos de cero (que correspondería al origen de coordenadas, que no pertenece al dominio de la función), y observa que la función es continua para cualquier valor de r o de θ.

Luego, observa las opciones para el segundo factor:

a)

sen(2θ) = 0, para: θ = 0, π/2, π, 3π/2, 2π,

y observa que la función toma el valor 0 para estos valores de θ,

por lo que tienes que 0 pertenece al rango de la función;

b)

sen(2θ) > 0, para los intervalos: (0,π/2), (π,3π/2),

y observa que cuando r tiende a 0 tienes que la expresión de la función tiende a cero,

y observa que cuando r tiende a +∞ tienes que la expresión de la función tiende a +∞,

por lo que tienes que el intervalo (0,+∞) está incluido en el rango de la función;

c)

sen(2θ) < 0, para los intervalos: (π/2,π), (3π/2,2π),

y observa que cuando r tiende a 0 tienes que la expresión de la función tiende a cero,

y observa que cuando r tiende a +∞ tienes que la expresión de la función tiende a -∞,

por lo que tienes que el intervalo (-∞,0) está incluido en el rango de la función.

Luego, tienes que el rango de la función es:

{0} u (0,+∞) u (-∞,0) = (-∞,+∞) = R (conjunto de los números reales).

Espero haberte ayudado.

Tienes la expresión de la función (a la que consideramos como derivada de orden 0):

f(x) = (1 - x)^-1 = 0!*(1 - x)^-1, que para x₀ = 0 toma el valor: f⁽⁰⁾0) = 0!;

luego, plantea algunas derivadas:

f⁽¹⁾(x) = (1 - x)^-2= 1!*(1 - x)^-2 que para x₀ = 0 toma el valor: f⁽¹⁾(0) = 1!;

f⁽²⁾(x) = 2*(1 - x)^-3 = 2!*(1 - x)^-3, que para x₀ = 0 toma el valor: f⁽²⁾(0) = 2!;

f⁽³⁾(x) = 6*(1 - x)^-4 = 3!*(1 - x)^-4, que para x₀ = 0 toma el valor: f⁽³⁾(0) = 3!;

f⁽⁴⁾(x) = 24*(1 - x)^-5 = 4!*(1 - x)^-5, que para x₀ = 0 toma el valor: f⁽⁴⁾(0) = 4!;

luego, observa que la expresión de la derivada general de orden k queda:

f^(k)(x) = k!*(1 - x)^-(k+1), que para x₀ = 0 toma el valor: f^(k)(0) = k!;

luego, recuerda que construyes la expresión del Polinomio de Taylor con valores de k entre 0 y n.

Luego, plantea la expresión de la derivada siguiente (orden n+1), para plantear la expresión del Resto de Lagrange:

f⁽ⁿ⁺¹⁾(x) = (n+1)!*(1 - x)^-(n+2), que evaluada para un valor z perteneciente al intervalo [0 , 0,5] queda: f⁽ⁿ⁺¹⁾(z) = (n+1)!*(1 - z)^-(n+2) = (n+1)!*/(1 - z)ⁿ⁺²;

luego, plantea la expresión del Resto de Lagrange:

R_n(x) = f⁽ⁿ⁺¹⁾(z)*(x - x₀)ⁿ⁺¹/(n+1)! = ( (n+1)!*/(1 - z)ⁿ⁺² )*(x - 0)ⁿ⁺¹/(n+1)! = xⁿ⁺¹/ (1 - z)ⁿ⁺²,con z ∈ [0 , 0,5].

Luego, para acotar el resto, plantea la expresión de su valor absoluto (observa que debemos estimarlo, sin importar si el error cometido es por defecto o por exceso):

| R_n(x) | < 10^-t,

sustituye expresiones y valore, y queda:

| xⁿ⁺¹/ (1 - z)ⁿ⁺² | < 10^-8,

observa que el argumento del valor absoluto es positivo para valores de x o de z pertenecientes al intervalo [0 ; 0,5], por lo que la inecuación queda:

xⁿ⁺¹/ (1 - z)ⁿ⁺² < 10^-8,

observa que el denominador del primer miembro toma su valor mínimo (lo que hace que el valor de la expresión sea máximo) para el extremo izquierdo del intervalo (z = 0), por lo que puedes plantear:

|R_n(x)| = xⁿ⁺¹/ (1 - z)ⁿ⁺² ≤ xⁿ⁺¹/ (1 - 0)ⁿ⁺² = xⁿ⁺¹/ 1ⁿ⁺² = xⁿ⁺¹/ 1 = xⁿ⁺¹;

observa que la expresión final se hace máxima para el extremos derecho del intervalo (x = 0,5), por lo que queda:

|R_n(x)| ≤ (0,5)ⁿ⁺¹ = (1/2)ⁿ⁺¹ = 1/2ⁿ⁺¹ (cota de error máxima).

Luego, para estimar  el grado del Polinomio de Taylor (n), plantea la condición del enunciado para la cota de error máxima:

1/2ⁿ⁺¹ < 10^-8,

multiplicas en ambos miembros por 10⁸ (observa que no cambia la desigualdad) y queda:

10⁸/2ⁿ⁺¹ < 1,

multiplicas en ambo miembros por 2ⁿ⁺¹ (observa que no cambia la desigualdad) y queda:

10⁸ < 2ⁿ⁺¹.

Luego, a fin de determinar grado del Polinomio de Taylor, comienza por componer con la función logaritmo natural en ambos miembros de la inecuación (observa que la función logaritmo natural es estrictamente creciente, por lo que no cambia la desigualdad):

ln(10⁸) < ln(2ⁿ⁺¹),

aplicas la propiedad del logaritmo de una potencia en ambos miembros y queda:

8*ln(10) < (n + 1)*ln(2),

haces pasaje de factor como divisor y queda:

8*ln(10)/ln(2) < n + 1,

haces pasaje de término y queda:

8*ln(10)/ln(2) - 1 < n, 

escribes la inecuación tal como la puedes leer de derecha a izquierda y tienes:

n > 8*ln(10)/ln(2) - 1 ≅ 25,6,

por lo que puedes concluir que el grado del Polinomio debe ser n = 26 o mayor, 

a fin de poder estimar los valores que toma la función en el intervalo [0 ; 0,5] con error menor que 10^-8.

Espero haberte ayudado.

la explicita de una recta es  y=mx+b   , si calculas m , la pendiente, te falta calcular la constante b

A partir de la ecuacion general   Ax+By+C=0

By=-C-Ax      y=-C/B-A/B x     m=-A/B     b=-C/B

Gracias

el primero ya en el primer renglón esta mal, fíjate la distributiva primera

La segunda esta bien

y con respecto a la tercera, esta mal la primer distributiva

Te voy a dejar las respuestas:

a) 2x² - 3x + 5xy + 5y²  (te equivocaste en desarrollar algo por ahí porque veo que en tu desarrollo te saltaste algunos pasos)

b) 2x² + 8xy

c) x - 2y

Como ves vas bastante bien si tuviste 2 buenas de 3, la noción del desarrollo algebraico ya lo tienes, ahora preocúpate de ir desarrollando paso a paso los ejercicios para no equivocarte en detalles pequeños. Cualquier otra duda, aquí estamos para eso.

Muchas gracias!!!

Hola Miguel, antes que nada hay que entender que en física la ecuación itinerario de posición X(t) si uno lo deriva con respecto al tiempo obtiene la ecuación de velocidad V(t) y si uno deriva la ecuación de velocidad con respecto al tiempo obtiene la aceleración A(t) la cual es constante.

Para resolverlo debes hacer lo siguiente:

- Para obtener V(t) integras A(t) con respecto a t → V(t) = ∫A(t) dt (como es una función vectorial solo debes integrar cada una de sus componentes):

∫A(t) = ( ∫0dt , ∫0dt , ∫-10dt ) = ( C1 , C2 , -10t + C3) 

Como son integrales indefinidas te quedan las constantes de integración, pero estas las obtienes reemplazando la velocidad incial V(0) entregada:

V(0) = ( C1 , C2 , -10*0 + C3) = (1,1,0) → C1 = C2 = 1 ; C3 = 0

Por lo que el vector velocidad resulta → V(t) = ( 1 , 1 , -10t )

-Para obtener R(t) integras V(t) con respecto a t → R(t) = ∫V(t) dt (básicamente haces lo mismo que antes):

∫V(t) = ( ∫1dt , ∫1dt , ∫-10tdt ) = ( t + C1 , t + C2 , (-10/2)t² + C3) = ( t  + C1 , t + C2 , -5t² + C3)

Para obtener las constantes de integración reemplazas la posición inicial R(0) entregada:

R(0) = ( 0+C1 , 0+C2 , -5*0²+C3 ) = ( 0 , 0 , 0 ) → C1 = C2 = C3 = 0

Por lo que el vector posición resulta → R(t) = ( t , t , -5t² )

Espero haberte ayudado, cualquier otra aquí estamos.

Tu duda des de física, para la próxima vez por favor deja cada duda en sus asignatura correspondiente. Por otro lado, tienes un video identico... 

pon tu duda en el foro de física!

gráficamente el Dom esta mal, ten en cuenta que lo de dentro de la raíz debe ser mayor a cero, pero el denominador no puede ser cero.

El primero correcto

el segundo  

Muchas gracias!!!

tengo el siguiente ejercicio y no me dá ¿podrias ayudarme?

(2y+x).(2y-x) + (x+y)² - x (y+3)   tendría que dar x-2y

a mi me dá 5y²-xy -3x