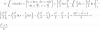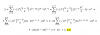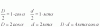Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Guillem De La Calle Vicente
el 26/8/17

Si f(x)=x+5 y g(x)=x²-3, calcule lo siguiente:
(a) f(f(x))
(b) g∘g(x)

••0 voto/s
•
Ángel
el 26/8/17
f(f(x))= f∘f(x) = x+5+5 = x+10
g∘g(x)= (x²-3)²-3 = x⁴+9-6x²-3 = x⁴-6x²+6

•0 voto/s
•
Desencadenado
el 26/8/17
fof=x+5=(x+5)+5=x+5+5=x+10

•0 voto/s
•
Desencadenado
el 26/8/17
gog = x^2-3 = (x^2-3)^2-3 = x^4-6x^2+9-3 = x^4-6x^2+6

•0 voto/s
•
Ángel
el 26/8/17
fof ≠ x+5 ≠ (x+5)+5
gog ≠ x^2-3 ≠ (x^2-3)^2-3

•0 voto/s
•
David
el 28/8/17
Composicion de funciones y Funcion Inversa
•0 voto/s
•

Cancelar
sheyla
el 25/8/17

35 alumnos se enfrentan a su examen final ordinario. hasta la fecha han aprobado el 70% de los casos sin tener en cuenta resultados anteriores ni alumnos concretos. cual es la probabilidad de que de los 35 alumnos...
a) aprueben mas de 15
b) y mas de 30?
c) y menos de 10?

••0 voto/s
•
Antonius Benedictus
el 26/8/17
Aproximacion de Binomial a Normal - Correccion de YATES Aproximacion de Binomial a Normal - Teorema de Moivre Laplace
•0 voto/s
•

Cancelar
Alba
el 25/8/17

Perdonen la torpeza pero no acabo de terminar el ejercicio, ¿me podrían explicar como han pasado de la primera integral a la segunda? Es que nunca he hecho una integral parcial con una función parecida.

Y mil gracias por intentar ayudarme aunque no me solucionen la duda por completo.

••0 voto/s
•
Guillem De La Calle Vicente
el 26/8/17

•1 voto/s
•

Cancelar
Sara
el 25/8/17

Hola necesito ayuda con todo este ejercicio..agradecería enormemente su ayuda.

••0 voto/s
•
Antonius Benedictus
el 25/8/17
Crecimiento y curvatura
Asíntotas
Continuidad de una función
Integrales definidas y área bajo una curva
•1 voto/s
•
Fermat
el 26/8/17
el apartado a) más un breve añadido sobre el estudio de la curvatura

•1 voto/s
•
Fermat
el 26/8/17
Aquí el b):

•1 voto/s
•
Fermat
el 26/8/17
el c):

•1 voto/s
•
Fermat
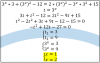
el 26/8/17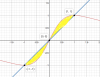
Sara, como no indicas en tu perfil que nivel de estudios tienes, no sé que herramientas de integración utilizas. Igual te extraña que utilice una doble integral (integral iterada) para el cálculo de áreas de regiones planas, te explico. Esa doble integral que puse representa el volumen del sólido formado por el recinto amarillo como base, paredes laterales verticales y como superficie superior la gráfica f(x,y)=1 (altura 1), esto equivale numéricamente al área de la región pedida. Espero que te ayude a comprender de dónde viene el procedimiento típico, si es que no lo sabías.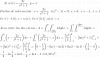

•1 voto/s
•
Fermat
el 26/8/17
Y el último Sara,

•1 voto/s
•

Cancelar
Christopher Halvorsen
el 25/8/17

me pueden ayudar con el ejercicio dos por favor
••0 voto/s
•
Antonius Benedictus
el 25/8/17

•0 voto/s
•

Cancelar
Manuel Perez
el 25/8/17

No consigo terminarlo, siempre termino con diferentes resultados

3^x*3+(3^x)²-12=2(3^x)²-3^x*3²+15

3t+t²-12=2t²-9t+15

2t²+12t+3=0 ????????

t₁=60 t₂=-72 ?????????

••0 voto/s
•
César
el 25/8/17

•1 voto/s
•
Desencadenado
el 25/8/17

•1 voto/s
•

Cancelar
Guillem De La Calle Vicente
el 25/8/17

Si f(x)=x+5 y g(x)=x²-3, calcule lo siguiente:
(a) f∘f(-5)
(b) g(g(2))

••0 voto/s
•
Desencadenado
el 25/8/17

•0 voto/s
•
Desencadenado
el 25/8/17

•0 voto/s
•

Cancelar
Andrea hdz
el 25/8/17

Ayuda con esta cuestión : en que ocasiones se cumple que el módulo de un número complejo es negativo?
Gracias!
••0 voto/s
•
Antonio Silvio Palmitano
el 25/8/17
Observa la definición de módulo de un número complejo (z = x + yi, con x e y números reales):
||z|| = |√(x²+y²)| = √(x²+y²),
y tienes que el módulo del numero complejo siempre es mayor o igual que cero (positivo).
Espero haberte ayudado.

•0 voto/s
•
Guillem De La Calle Vicente
el 25/8/17
Nunca. Por definición es no-negativo.
Es como si cogieras la norma de un vector.
Saludos.

•0 voto/s
•

Cancelar
Hugo
el 25/8/17

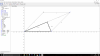
Hola, no encuentro una relación para llegar a que las diagonales de este rombo miden 2sen(α) y 2cos(α).
Se agradece mucho la ayuda.
Saludos!

••0 voto/s
•
César
el 25/8/17

•1 voto/s
•
Antonio Silvio Palmitano
el 25/8/17
Considera el triángulo rectángulo en el que tienes indicado el ángulo α y la longitud de un lado del rombo (L = 1 cm),
y observa que la longitud del cateto adyacente al ángulo es la mitad de la longitud de la diagonal mayor (ad = D/2), observa que la longitud del cateto opuesto al ángulo es la mitad de la longitud de la diagonal menor (op = d/2), y observa que la longitud de la hipotenusa del triángulo es L = 1 cm.
Luego, plantea las relaciones trigonométricas:
ad/L = cosα, haces pasaje de divisor como factor y queda:
ad = L*cosα, sustituyes en el primer miembro y queda:
D/2 = L*cosα, haces pasaje de divisor como factor y queda:
D = 2*L*cosα, que es la longitud de la diagonal mayor del rombo;
op/L = senα, haces pasaje de divisor como factor y queda:
op = L*senα, sustituyes en el primer miembro y queda:
d/2 = L*senα, haces pasaje de divisor como factor y queda:
d = 2*L*senα, que es la longitud de la diagonal menor del rombo.
Luego, puedes plantear para el producto de las diagonales del rombo:
P = D*d, sustituyes expresiones y queda:
P = 2*L*cosα*2*L*senα, simplificas coeficientes, ordenas factores y queda:
P = 2*L²*2*cosα*senα,
aplicas la identidad trigonométrica del seno del doble de un ángulo (sen(2*α) = 2*cosα*senα) y queda:
P = 2*L²*sen(2*α).
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Pablo
el 25/8/17

Hola, he hallado el rango de esta matriz 3×5 y me ha dado dos, pero el procedimiento es muy lioso y no me entero, si y me pueden ayudar lo agradecería. Gracias de antemano

••0 voto/s
•
Guillem De La Calle Vicente
el 25/8/17

•0 voto/s
•

Cancelar