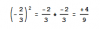-
stefany
el 17/6/17Podéis Ayudarme con esta derivada, gracias
Antonio Silvio Palmitano
el 17/6/17Observa que puedes reescribir la expresión de la función:
f(x) = ( (3x+1)/(x+2) )1/2 = (3x+1)1/2 / (x+2)1/2 = (3x+1)1/2 * (x+2)-1/2 = u*v
Luego, plantea las derivadas de los factores (observa que debes aplicar la regla de la cadena):
u ' = (1/2)*(3x+1)-1/2*3 = (3/2)*(3x+1)-1/2
v ' = - (1/2)*(x+2)-3/2*1 = - (1/2)*(x+2)-3/2
Luego aplicas la regla de un producto y queda:
f ' (x) = u ' * v + u * v '
sustituyes las expresiones de los factores en cada término y queda:
f ' (x) = (3/2)*(3x+1)-1/2 * (x+2)-1/2 + (3x+1)1/2 * ( - (1/2)*(x+2)-3/2 ) = (3/2) * (3x+1)-1/2 * (x+2)-1/2 - (1/2) * (3x+1)1/2 * (x+2)-3/2 .
Espero haberte ayudado.
-
Albano Caminos
el 17/6/17 -
Fernando Navarro
el 17/6/17Buenas, me podes ayudar en este ejercicio?
Determine la posición relativa de los siguientes objetos:
π1: x+y+√2*z=1 y π2: x+y=5
Antonio Silvio Palmitano
el 17/6/17Tienes las ecuaciones cartesianas implícitas de dos planos, cuyos vectores normales quedan expresados:
n1 = <1,1,√(2)> y n2 = <1,1,0>.
Observa que los vectores normales no son paralelos (plantea el producto vectorial entre ellos):
n1 x n2 = <-√(2),√(2),0> ≠ <0,0,0>.
Por lo tanto, tienes que los planos se cortan en una recta, cuyo vector director queda expresado:
u = n1 x n2 = <-√(2),√(2),0>.
Luego, plantea el sistema formado por las ecuaciones de los planos, a fin de determinar un punto de la recta:
x + y + √(2)z=1
x + y = 5
Observa que tienes un sistema de dos ecuaciones con tres incógnitas, por lo que puedes determinar un valor para una de ellas,
por ejemplo para x = 0 el sistema queda:
y + √(2)z = 1
y = 5
Reemplazas el valor remarcado en la primera ecuación y queda:
5 + √(2)z = 1, haces pasaje de término y queda:
√(2)z = - 4, multiplicas por √(2) en ambos miembros y queda:
2z = - 4√(2), haces pasaje de factor como divisor y queda:
z = - 2√(2).
Luego, con los valores remarcados tienes las coordenadas de un punto de la recta: A( 0 , 5 , -2√(2) ).
Luego, con el punto A y el vector director u puedes plantear las ecuaciones cartesianas paramétricas de la recta,
que es la intersección entre los planos cuyas ecuaciones tienes en el enunciado:
x = 0 - √(2)t
y = 5 + √(2)t
z = -2√(2) + 0t,
con t ∈ R.
Espero haberte ayudado.
-
Fernando larruscain
el 17/6/17hola , podrian resolver esto: (2xcuadrado+1)cuadrado - (2xcuadrado+1) · (2xcuadrado-1)
Antonio Silvio Palmitano
el 17/6/17Tienes la expresión algebraica:
(2x2 + 1)2 - (2x2 + 1)*(2x2 - 1) =
desarrollas el binomio elevado al cuadrado en el primer término, distribuyes en el segundo término y queda:
= 4x4 + 4x2 + 1 - (4x4 - 2x2 + 2x2 - 1) =
cancelas términos opuestos en el agrupamiento, luego distribuyes el signo en el agrupamiento y queda:
= 4x4 + 4x2 + 1 - 4x4 + 1 =
cancelas términos opuestos, reduces términos numéricos y queda:
= 4x2 + 2 = 2(2x2 + 1).
Otra forma.
Tienes la expresión algebraica:
(2x2 + 1)2 - (2x2 + 1)*(2x2 - 1) =
extraes factor común (2x2 + 1) y queda:
= (2x2 + 1)*( (2x2 + 1) - (2x2 - 1) ) =
distribuyes agrupamientos en el segundo factor y queda:
= (2x2 + 1)*( 2x2 + 1 - 2x2 + 1 ) =
cancelas términos opuestos y reduces términos semejantes en el segundo factor y queda:
= (2x2 + 1)*( 2 ) = = 2(2x2 + 1).
Espero haberte ayudado.
-
Fernando larruscain
el 17/6/17hola, (-2/3)al cuadrado. cuanto daria ?-4/9 o -9/4
-
stefany
el 17/6/17Hola podéis Ayudarme a resolver estas derivadas
Antonio Silvio Palmitano
el 17/6/17Tienes la expresión de la función (observa que tienes un producto):
f(x) = 24x^2-1*ln(8x) = u*v.
Luego, plantea las derivadas para cada factor (observa que debes aplicar la regla de la cadena):
u ' = 24x^2-1*(4*2x - 0) = 8x*24x^2-1
v ' = ( 1 / 8x )*8 = 1/x.
Luego aplicas la regla de derivación para un producto de funciones y queda:
f ' (x) = u ' * v + u * v ', sustituyes expresiones y queda:
f ' (x) = 8x*24x^2-1 * ln(8x) + 24x^2-1 * 1/x.
Espero haberte ayudado.
-
Jean Anthony
el 17/6/17A un florista le han encargado preparar 5 ramos iguales para cinco eventos. El precio total acordado es de 610 euros. Ha decidido emplear rosas, tulipanes y lilas. Cada ramo lleva un total de 24 flores y el número de rosas empleado doblara al número total de flores de otras especies. ¿Cual es el número de flores de cada tipo que usará en cada ramo sabiendo que cada rosa cuesta 6€, cada tulipán 4€ y cada lila 3€?
-
Oscar Robles
el 17/6/17Buenas tardes comunidad, tengo un examen pronto y necesito enterarme sobre las funciones homogéneas, no tengo claro lo que es pero creo que son las que tienen mas de una variable no? Como se analizan estas funciones? no he podido encontrar ningún vídeo al respecto. Necesito saber como sacar el dominio,asintotas, rango/recorrido de estas funciones y en definitiva , un análisis completo de las funciones homogéneas y representarlas. Esto es para la asignatura de Matemáticas 1 en la carrera de economía, por favor ayudadme.
-
Fran Cescrack
el 17/6/17
Buenas alguien me ayuda con el siguiente ejercicio? tengo exámen final el lunes y este tipo de ejercicios se me resisten
Antonius Benedictus
el 17/6/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
