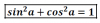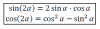Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

AlexG
el 17/6/17

Hola tengo una duda sencilla con este ejercicio:se refiere a calcular el volumen de esta piramide y :no se si es con esta formula (Volumen=1/3base*h) o volumen=(b*h dividido entre 3) que seria 490*280/3=volumen(41066,6 cm3) lo tengo hecho de estas dos formas,estaría bien la primera forma?
Muchas gracias.

••0 voto/s
•
Antonio Silvio Palmitano
el 17/6/17
La expresión del volumen de una pirámide que has empleado es la correcta: V = (1/3)*(Superficie de la base)*(altura) = (1/3)*S_B*h,
y como tienes que la base es cuadrada, su superficie queda expresada: S_B = (arista de la base)²= a_B².
Espero haberte ayudado.

•1 voto/s
•
AlexG
el 17/6/17
Es decir arista de la base=AB=440 al cuadrado
y volumen te da como resultado:18.069.240 m3

•0 voto/s
•
Antonio Silvio Palmitano
el 17/6/17
Tal cuál has resuelto:
Superficie de la base: S_B = a_B² = (440 m)² = 193600 m².
Luego, tienes:
V = (1/3)*S_B*h = (1/3)*(193600 m²)*(280 m) = (1/3)*54208000 m³≅ 18069333,333 m³.
Espero haberte ayudado.

•1 voto/s
•
AlexG
el 17/6/17
Muchas gracias

•0 voto/s
•

Cancelar
Usuario eliminado
el 17/6/17

Hola, ¿podéis ayudarme con el último apartado del ejercicio que he adjuntado?
Si hago una P(384) me sale muy complicado.

••0 voto/s
•
Antonius Benedictus
el 17/6/17
http://www.itchihuahua.edu.mx/academic/industrial/sabaticorita/_private/05Distr%20Poisson.htm
¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

•0 voto/s
•

Cancelar
fernando
el 17/6/17

Una duda sencilla, en el metodo gauss cuando cojes un numero negativo vamos a decir -X a la hora de poner -F1 + 2F2 (ejemplo simplemente) si el el -x es negativo, entonces cambiaria el signo del F1? seria F1+F2?

••0 voto/s
•
Antonius Benedictus
el 17/6/17
No te explicas bien o no te entendemos bien, Fernando. Reformula la pregunta y añade un ejemplo.

•0 voto/s
•
fernando
el 17/6/17

Me refiero a esto. Cuando pones Si cojo el -x para la primera fila ( -F1 +F2 ) Seria correcto? o al - - = +?

•0 voto/s
•
Antonius Benedictus
el 17/6/17
A ver si te aclaro algo:

•0 voto/s
•

Cancelar
Samuel Ruiz
el 17/6/17

Podrían ayudarme a resolver este problema por integración doble?, por triple si me sale pero por integración doble con cambio de variable no

••0 voto/s
•
Antonius Benedictus
el 17/6/17
¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

•0 voto/s
•
Antonio Silvio Palmitano
el 17/6/17
Vamos con una orientación.
Tienes un sólido B que es la cuarta parte de un elipsoide macizo.
Plantea un sistema de coordenadas tridimensional cartesiano OXYZ usual (eje OX "hacia adelante y atrás", eje OY "hacia la derecha e izquierda", eje OZ "hacia arriba y abajo").
Observa que el sólido está limitado por el plano OXY "por debajo", el plano OYZ "por derecha" y el elipsoide "por arriba".
Luego, observa que la base del sólido (R) es un semidisco elíptico en el plano OXY, que se encuentra en el segundo y en el tercer cuadrante, que queda descrito:
x²/9 + y²/4 = 1
z = 0
y ≤ 0,
y observa que la ecuación cartesiana explícita del elipsoide queda:
z = f(x,y) = 1 - x²/9 - y²/4, que puedes escribir en la forma: z = f(x,y) = 1 - (x/2)² - (y/3)².
Luego, puedes plantear para el cálculo del volumen:
V_B = ∫∫_R f(x,y)*dx*dy = ∫∫_R ( 1 - (x/2)² - (y/3)² )*dx*dy (1).
Luego, puedes plantear el cambio de coordenadas:
x/3 = u, de donde despejas: x = 3u, con -1 ≤ u ≤ 1 (observa que los valores extremos para x son - 3 y 3),
y/2 = v, de donde despejas: y = 2v, con -1 ≤ v ≤ 1 (observa que los valores extremos para y son: - 2 y 2),
cuyo factor de compensación (jacobiano) queda: |J| = 3*2 = 6.
Luego, aplicas el cambio de coordenadas y la integral señalada (1) queda:
V_B = ∫∫_R ( 1 - u² - v² )*6*du*dv = 6* ∫∫_R ( 1 - u² - v² )*du*dv (2).
Luego, puedes plantear el cambio a coordenadas polares:
u = r*cosθ
v = r*senθ,
con 0 ≤ r ≤ 1, π/2 ≤ θ ≤ 3π/2,
cuyo factor de compensación (Jacobiano) queda: |J| = r.
Luego, aplicas el cambio de coordenadas y la integral señalada (2) queda:
V_B = 6* ∫∫_R ( 1 - r² )*r*du*dv = 6* ∫∫_R ( r - r³ )*dr*dθ = y puedes continuar la tarea.
Observa que, desde el punto de vista geométrico, tienes inicialmente una región de integración R que es un semidisco elíptico, que con la primera transformación (cambios de escalas) se transforma en en un semicírculo de radio igual a uno, y luego aplicas el cambio a coordenadas polares.
Espero haberte ayudado.

•1 voto/s
•
Samuel Ruiz
el 17/6/17
Si, muchas gracias; ya veo donde me equivocaba muchas gracias por la explicación Antonio

•0 voto/s
•

Cancelar
Evi
el 17/6/17

(X½)/X-1
Buenos dias david, me podrias resolver esta ecuacion por favor, es que la he hecho varias veces, y varias veces me han salido resultados de la grafica diferentes.
Muchas Gracias.
saludos

••0 voto/s
•
Antonius Benedictus
el 17/6/17
Pon la foto original, pues me temo que la ecuación no está bien transcrita. Para empezar, falta el signo =.

•0 voto/s
•

Cancelar
Álvaro
el 17/6/17

Buenos días, ayuda con esta operación.
Simplifica la siguiente expresión trigonométrica:

••0 voto/s
•
Antonius Benedictus
el 17/6/17

•0 voto/s
•

Cancelar
Alejandro Expósito
el 17/6/17

calcula el el termino general de una progresión aritmética apartir de a₅=27 y a₁₂=48
Alguien me puede explicar este ejercicio paso a paso

••0 voto/s
•
Antonius Benedictus
el 17/6/17

•0 voto/s
•

Cancelar
Elena
el 17/6/17

Hola!
Si tengo un logaritmo neperiano con signo negativo, y lo quiero quitar con la propiedad de elevarlo al numero e, ¿ qué hago con el signo negativo?
Gracias!

••0 voto/s
•
Antonius Benedictus
el 17/6/17
Pon mejor el supuesto práctico y te lo explicamos.

•0 voto/s
•
Elena
el 17/6/17
Sería despejar la y , pero no sé qué tendría que hacer con el signo negativo del Ln
Gracias!

•0 voto/s
•
Antonius Benedictus
el 17/6/17

•0 voto/s
•

Cancelar
Álvaro
el 17/6/17

Simplifica la siguiente expresión trigonométrica:

••0 voto/s
•
Antonius Benedictus
el 17/6/17

•0 voto/s
•

Cancelar
Álvaro
el 17/6/17

El valor de en función del ángulo es:
Explicación
Obtención:

••0 voto/s
•
Antonius Benedictus
el 17/6/17
Fórmulas usadas:
Diferencia de cuadrados.
Identidad fundamental:

Seno y coseno del ángulo doble:

•0 voto/s
•

Cancelar