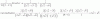¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

parece estar bien almenos por lo que he podido mirar sii esta bien aunque yo si fuese tu repasaría ms los infinitos

te ha servido?

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

Observa que debes determinar las coordenadas de un punto P(x,y) perteneciente a la curva cuya ecuación es y = x² + 1 (1),

cuya distancia al punto A(3,1) sea mínima

Luego, puedes plantear la expresión de la función "distancia elevada al cuadrado":

f(x,y) = d(A,P)² = (x - 3)² + (y - 1)², 

luego sustituyes la expresión señalada (1) y queda:

f(x) = (x - 3)² + (x² + 1 - 1)² = (x - 3)² + (x²)² = (x - 3)² + x⁴.

Luego, plantea la expresión de la derivada primera:

f ' (x) = 2(x - 3) + 4x³ = 2x - 6 + 4x³ = 4x³ + 2x - 6.

Luego, plantea la expresión de la derivada segunda:

f ' ' (x) = 12x² + 2.

Luego, plantea la condición de punto crítico (posible máximo o posible mínimo)

f ' (x) = 0, sustituyes y queda:

4x³ + 2x - 6 = 0, divides por 2 en todos los términos de la ecuación y queda:

2x³ + x - 3 = 0, observa que x = 1 es una raíz, factorizas por medio de la Regla de Ruffini y queda:

(x - 1)*(2x² + x + 3) = 0, observa que el segundo factor no tiene raíces reales, 

por lo tanto el punto crítico es: x = 1,

luego reemplazas en la expresión de la derivada segunda y queda:

f ' ' (1) = 12*1² + 2 = 14 > 0,

por lo que tienes que la gráfica de la función es cóncava hacia arriba,

por lo que presenta un mínimo en x = 1, al que le corresponde: y = 1² + 1 = 2,

por lo que las coordenadas del punto buscado son: P(1,2).

Luego reemplazas en la expresión de la función (recuerda que es la distancia del punto P al punto A elevada al cuadrado), y queda:

f(1) = (1 - 3)² + 1⁴ = (- 2)⁴ + 1 = 16 + 1 = 17,

luego tienes:

d(A,P)2 = 17, haces pasaje de potencia como raíz y queda: d(A,P) = √(17).

Espero haberte ayudado.

Empleamos la base canónica de R³.

f(1,0,0) = < 0 , 0 , 1 >,

f(0,1,0) = < 1 , 1 , 0 >,

f(0,0,1) = < -1 , 1 , 0 >;

luego, la matriz asociada a la aplicación lineal, en base canónica, queda:

A =

0    1   -1

0    1    1

1    0    0.

Luego, planteamos para un vector genérico perteneciente al núcleo de la aplicación:

f(x,y,z) = < 0 , 0 , 0 >, sustituyes y queda:

< y-z , y+z , x > = < 0 , 0 , 0 >, luego tienes, por igualdad entre vectores:

y - z = 0, de aquí despejas: y = z (1)

y + z = 0

x = 0,

luego, sustituyes la expresión señalada (1) en la segunda ecuación y queda:

2z = 0, haces pasaje de factor como divisor y queda: z = 0,

luego reemplazas en la ecuación señalada (1) y queda: y = 0;

por lo tanto, tienes que el núcleo de la aplicación queda:

N = { < x , y , z > ∈ R³ / x = 0, y = 0, z = 0 } = { < 0 , 0 , 0 > };

luego, su dimensión es: dim(N) = 0.

Luego, considera un vector genérico perteneciente a la imagen de la aplicación:

w = < y-z , y+z , x > = < 0 , 0 , x > + < y , y , 0 > + < -z , z , 0 >, extraes factores comunes escalares y queda:

w = x*< 0 , 0 , 1 > + y*< 1 , 1 , 0 > + z*< -1 , 1 , 0 >;

luego, puedes demostrar (te dejo la tarea) que los tres vectores son linealmente independientes,

por lo que una base de la imagen es: B_I = { < 0 , 0 , 1 > , < 1 , 1 , 0 > , < -1 , 1 , 0 > },

y su dimensión es: dim(I) = |B_I| = 3, por lo que tienes que la imagen es R³.

Espero haberte ayudado.

Miriam, depende de los datos de que dispongas. Sube un ejercicio que te resulte complicado sobre este asunto y te lo explicamos.

Hola primero debes calcular los sub-espacios del nucleo y de la imagen, luego buscar las bases de los mismo. Con eso ya puedes verificar el teorema de la dimension. Si necesitas ayuda para calcular los sub-espacios y las bases me dice y hago alguno de los apartados. Mi español es muy malo perdonar si cometi algún error.  

No entiendo como calcular los subespacios, podrias hacer un ejemplo para que vea a lo que te refieres? thanks

Integrales por cambio de variable