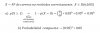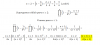-
 Alguien podría ayudarme a desarrollar la siguiente ecuación?,según la tengo en la imagen no entiendo ni el porque la desarrolla de esa manera ni como la desarrolla, estoy muy verde en esto y esta ecuación se me esta atragantando,agradeceria que alguien me la explicara, gracias
Alguien podría ayudarme a desarrollar la siguiente ecuación?,según la tengo en la imagen no entiendo ni el porque la desarrolla de esa manera ni como la desarrolla, estoy muy verde en esto y esta ecuación se me esta atragantando,agradeceria que alguien me la explicara, graciasAlejandro García Candelas
el 5/6/171. Primero desarrolla el paréntesis multiplicando cada uno de los componentes por -3, el primero es una división entre 3 también por lo que consigue es eliminar el denominador.
2.Opera lo que ha desarrollado en la izquierda, de tal modo que se le van 3x y -3x.
3.Multiplica a ambos lados de la ecuación todos los componentes por 2 para eliminar el denominador en a fracción de la izquierda.
4. Opera el paréntesis que le aparece y despeja la x agrupándolas, basta con saber en que consiste despejar cuando únicamente tenemos sumas restas y al final cuanto obtiene -3x=33 pasa el -3 dividiendo para retirarlo de la izquierda y operar para obtener el valor de x
ILDEFONSO
el 5/6/17 -
-
-
Alejandro García Candelas
el 5/6/17Salomón Hernández
el 5/6/17Alejandro García Candelas
el 5/6/17 -
Ángel
el 5/6/17Mediana: Si son 15 datos, los ordenas de menor a mayor. La mediana ocupa el puesto 8º, que es el del medio
Con los datos ordenador aprovechas para hallar:
*Cuartiles: http://www.vitutor.com/estadistica/descriptiva/a_11.html
*Percentiles: http://www.vitutor.com/estadistica/descriptiva/a_13.html
-
Antonio Silvio Palmitano
el 5/6/17Tienes la expresión del coste de fabricar x unidades: C(x) = (1/4)x2 + 35x + 25.
Tienes el precio de venta de una unidad: P = 60 - (1/4)x,
de donde tienes que la recaudación por vender x unidades es: R(x) = xP = x(60 - (1/4)x) = 60x - (1/4)x2.
Luego, plantea que el beneficio es igual a la diferencia entre la recaudación y el coste para x unidades:
B(x) = R(x) - C(x), sustituyes expresiones y queda
B(x) = (60x - (1/4)x2) - ((1/4)x2 + 35x + 25) = 60x - (1/4)x2 - (1/4)x2 - 35x - 25,
reduces términos semejantes y queda:
B(x) = - (1/2)x2 + 25x - 25,
que es la expresión del beneficio en función de la cantidad diaria de unidades producidas.
Luego derivas y queda:
B ' (x) = - x + 25,
luego planteas la condición de punto crítico (posible máximo o posible mínimo):
B ' (x ) = 0, sustituyes y queda:
- x + 25 = 0, haces pasaje de término y queda:
25 = x.
Luego, evaluamos en a expresión de la función beneficio para verificar:
B(24) = - (1/2)*242 + 25*24 - 25 = - 288 + 600 - 25 = 287 euros;
B(25) = - (1/2)*252 + 25*25 - 25 = - 312,5 + 625 - 25 = 287,5 euros;
B(26) = - (1/2)*262 + 25*26 - 25 = - 338 + 650 - 25 = 287 euros.
Espero haberte ayudado.
-
Cómo planteo y calculo el volumen de un sólido limitado inferiormente por x^2+y^2=z y superiormente por x^2+y^2=(z-6)^2
Hago cambio de variable a esféricas, a polares, o a cilíndricas?
Antonio Silvio Palmitano
el 5/6/17Observa que las superficies que limitan el sólido son un paraboloide con eje z, con vértice en el origen (superficie "inferior"), y un semicono con el punto de coordenadas: (0,0,6) (superficie superior).
Luego, observa que ambas superficies tienen eje de simetría z pero no tienen centro de simetría, por lo que tienes que el cambio de coordenadas más útil es pasar a Coordenadas Ciínricas con eje z:
x = r*cosθ
y = r*senθ
z = z,
con el factor de compensación (Jacobiano): |J| = r.
Luego, pasas las ecuaciones de ambas superficies a coordenadas cilíndricas y queda:
Si: z = r2,
Ss: r2 = (z -6)2, de donde puedes despejar: - r = z - 6, y luego tienes: - r + 6 = z. (observa que tomamos la raíz cuadrada negativa, ya que la superficie que limita superiormente al sólido es el semicono inferior.
Luego, los límites de integración para z quedan: r2 ≤ z ≤ (- r + 6).
Luego, para determinar la frontera de la región de proyección, igualamos las expresiones de las superficies que hemos remarcado y queda:
r2 = - r + 6, haces pasajes de términos y queda:
r2 + r - 6 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
r = - 3, que no tiene sentido para este problema (recuerda que r toma valores positivos),
r = 2, que es la ecuación (en coordenadas polares) de una circunferencia con centro en el origen del pano OXY, cuyo radio es igual a 2, por lo que los límites de integración que faltan determinar quedan:
0 ≤ r ≤ 2,
0 ≤ r ≤ 2π,
Luego, pasas al planteo del voumen:
V = ∫∫∫ 1*dx*dy*dz = planteas el cambio de coordenadas = ∫∫∫ 1*r*dz*dr*dθ = y puedes continuar la tarea.
Haz el intento, y si te es preciso, no dudes en volver a consultar.
Espero haberte ayudado.
-
Me ayudarían con este problema
Los tornillos adquiridos por una armadora de autos, tienen un peso medio de 5.02 gramos y una desviación estándar de 0.3 gramos. Encuentre la probabilidad de que una muestra aleatoria de 100 tornillos tenga un peso promedio entre 4.96 y 5.01 gramos?
gracias
Ángel
el 5/6/17