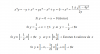-
Usuario eliminado
el 20/5/17 -
Valeria
el 20/5/17Hola buenas, si pudieran ayudarme con este ejercicio se los agradecería un montón!!. Es del modelo de selectividad de este año. Mi idea es sustituir t (tiempo) hasta obtener un valor no negativo > 0 (en tal caso 3). Luego, hacer el limite x ---> infinito que seria = 6, y podría afirmar que ese seria el máximo beneficio que obtendría la empresa. ¿Mi planteamiento estaría correcto?
-
Ángel Camps
el 20/5/17¿Alguien me podría ayudar con la función definida a trozos del ej 2 ?. He visto todos los vídeos pero ninguno es de este estilo.
Gracias!!
Antonio Silvio Palmitano
el 20/5/17Puedes plantear:
a)
f(t) > 0, sustituyes y queda:
(30t - 60)/(5t + 7) > 0, haces pasaje de divisor como factor (observa que el divisor es positivo para todo valor de t positivo) y queda:
30t - 60 > 0, haces pasaje de término y queda:
30t > 60, haces pasaje de factor como divisor y queda:
t > 2,
por lo que tienes que los beneficios son positivos a partir del tercer año.
b)
Lìm(t→+∞) f(t) = Lìm(t→+∞) (30t - 60)/(5t + 7) = extraes factores comunes en el numerador y en el denominador y queda:
= Lìm(t→+∞) t(30 - 60/t) / t(5 + 7/t) = simplificas y queda:
= Lìm(t→+∞) (30 + 60/t)/(5 + 6/t) = (30 + 0)/(5 + 0) = 30/5 = 6,
por lo que tienes que el límite superior de los beneficios es seis millones de euros.
Espero haberte ayudado.
-
James Junior Abreu Sosa
el 20/5/17Como se calcula la distancia entre 2 vectores sin esta formula d=√Δx2+Δy2+Δz2
Es que si hay alguna forma mas mecanica me gustaria saberlo
-
Guillem de la Calle
el 20/5/17La función de probabilidad f de una variable aleatoria discreta x es nula salvo en elos puntos 0,1 y 2; en ellos los valores f(10=4c cuadrado; f(1)=4c-10c cuadrado; f(2)=4c-1:
a) Determinar las valores en c.
b) Hallar la función de probabilidad y la función de distribución.
Recuerde que la suma de probabilidades es 1.
-
Ivanconstan
el 20/5/17 -
Guillem de la Calle
el 20/5/17Demuestra o refuta la siguiente propiedad:
Para cada real y existe un único real x tal que x⁴y=x²-y.
Antonio Silvio Palmitano
el 20/5/17Haces pasajes de tèrminos y tienes la ecuación polinómica:
yx4 - x2 + y = 0
Luego, para y = 1/16 reemplazas y tienes:
x4/16 - x2 + 1/16 = 0
Multiplicas por 16 en todos los términos y queda:
x4 - 16x2 + 1 = 0
que es una ecuación polinómica bicuadrática cuyas soluciones para x2 son:
1) x2 = ( 16 - √(252) )/2 = 8 - √(63) > 0, por lo que tienes dos opciones para x;
2) x2 = (16 + √(252))/2 = 8 + √(63) > 0, por lo que tienes otras dos opciones para x.
Espero haberte ayudado.
-
Julia
el 20/5/17Buenos días, en este ejercicio me piden que halle el punto o puntos de r que equidistan de π1 y π2.
Yo he sacado P de la intersección de r y π1 y Q de la intersección de π2 y he sacado el punto medio pero no me da...
Me podeis decir donde he fallado? Muchas gracias
-
Periko
el 20/5/17 -
Paula Sánchez
el 20/5/17Estarían bien factorizados los polinomios;
(x 4 - 1) = (x-1)(x+1) x²
(x³ + 1) = (x-1) (x+1) x
Victor
el 20/5/17No, los dos polinomios están mal factorizados.
Si muestras tu resolución del ejercicio podremos decirte dónde te equivocaste, de otra manera solo podemos decirte cómo se resuelve y el resultado.
(x^4-1) = (x+1) (x-1) (x^2+1)
(x^3+1) = (x+1) (x^2-x+1)
Para poder corregirte a ti misma este tipo de ejercicios, asigna a x un valor. El resultado de un lado de la ecuación tiene que ser idéntico al resultado del otro lado de la ecuación.
Para x=2, a ti te da este resultado en ambos lados:
15 = 12
9 = 6
Como puedes comprobar esas igualdades son FALSAS.
