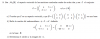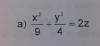-
Flor Torres
el 19/5/17 -
Jose Lopez
el 19/5/17 -
Fernando Navarro
el 19/5/17Determinar el valor de las y ∈ℛ para que el siguiente sistema tenga solución
x1+ 4x2+ 5x3= y1
2x1+ 3x2+ 5x3= y2
x1+ 9x2+ 10x3= y3
llegue a:
101 -1/5y1+ 4/5y2
011 2/5y1 - 1/5y2
000 -3y1+ y2+ y3
A partir de aquí no se como continuar para realizar el enunciado
Antonio Silvio Palmitano
el 19/5/17Empleamos el Método de Gauss.
1 4 5 y1
2 3 5 y2
1 9 10 y3
a la segunda fila le restamos el doble de la primera, a la tercera fila le restamos la primera y queda:
1 4 5 y1
0 -5 -5 y2 - 2y1
0 5 5 y3 - y1
a la tercera fila le sumamos la segunda y queda:
1 4 5 y1
0 -5 -5 y2 - 2y1
0 0 0 y3 + y2 - 3y1
Luego, para que el sistema tenga solución, debe cumplirse que la tercera fila de la matriz ampliada sea nula, para lo que planteamos:
y3 + y2 - 3y1 = 0,
de donde podemos despejar:
y3 = 3y1 - y2,
Por lo tanto, concluimos que existen infinitos valores para y1, y2 e y3 que cumplen con la igualdad remarcada.
Espero haberte ayudado.
-
Julia
el 19/5/17Hola buenas tardes, ¿me podríais ayudar con el siguiente determinante? Muchas gracias.
Ángel
el 19/5/17 -
Pamela Zambrano
el 19/5/17 -
Sandra López Gómez
el 19/5/17Buenas, tengo un problema de volúmenes:
A partir de un trozo cuadrado de papel, construir una caja sin tapa, cortando cuadrados iguales en las esquinas. ¿Hay cortes que produzcan determinado volumen? ¿Qué longitud del lado del cuadrado produce volumen máximo? ¿Hay cortes diferentes que produzcan el mismo volumen de la caja?
¡Gracias!
-
Flor Torres
el 19/5/17 -
Javier Marquez
el 19/5/17Hola, tengo una pequeña duda de sumatorias, estan bn los pasos q hice?Gracias de antemano
Antonio Silvio Palmitano
el 19/5/17 -
Paula Sánchez
el 19/5/17Tengo que representar los límites y eso que hay arriba de la gráfica, la gráfica es el ejercicio resuelto por el profesor. Y mi duda es que porque está la línea morada que está redondeada, si es creciente hasta uno
-
Jonnathan Caicedo
el 19/5/17
Buen día. Por lo que leo y he buscado no hay vídeos para el tema de Cuádricas o Geometría en R3. Sabiendo la formula y la teoría, tengo problemas para entender como hallar las trazas y las intersecciones con los ejes coordenados en diferentes superficies espaciales cuando hay valores numéricos. Un ejemplo es como el siguiente caso:
Les agradezco si me ayudan a entender cómo usar los valores para gráficar. Y si hacen un vídeo para tratar figuras espaciales nos ayudarían a muchos.
Gracias por su tiempo y atención.
Antonius Benedictus
el 31/5/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
