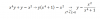-
Omar
el 20/5/17Hola, alguien sabría cómo resolver este ejercicio si no está mal planteado? Necesito estudiar la posición relativa en función de ."a"..
Me dan 2 puntos de cada recta, el Pr (5,1,6) y el Ps(0,0,-6) que hallando vector que los une, obtengo PrPs" (-5,-1,-12)
y luego me dan 2 planos en forma de un sistema: ax + 3y+2z =12 ; 2x +5y-z = 6
-
Paula Sánchez
el 20/5/17Porqué el apartado h) el resultado es -infinito en vez de infinito?
Es Una indeterminación del tipo infinito partido de infinito. Por tanto, como el grado mas alto de x arriba es x elevado a 3, sería - infinito, como acabo es elevado a dos, sería más infinito, por tanto -infinito/+infinito es igual a menos infinito, no entiendo entonces por qué el resultado es más infinito
MUCHÍSIMAS GRACIAS!!
Victor
el 20/5/17Porque el numerador es de grado superior al numerador ya sabemos que va a dar + o - infinito. El límite dice que tiende a -infinito.
Si sustituyes x^3 por menos infinito te dará -infinito.
Si fuese x^2 te daría +infinito, porque (-1)*(-1)=+1
Si tengo algo mal que alguien me corrija, gracias.
-
Abril
el 20/5/17Hola. En el apartado b) de este ejercicio, ¿por qué el vector es (1,0,-2)?
Victor
el 20/5/17Lo que más me asusta es que en la resolución ha utilizado la fórmula de la ecuación continua cuando uno de los componentes del vector es nulo (0). Esa forma solo se puede utilizar si ningún componente es nulo.
Cuando tenemos expresado un plano con su fórmula general, el vector normal a ese plano (el perpendicular) se puede obtener directamente del plano. En ese caso concreto el plano es x +0y -2z +3 = 0. Los componentes del vector NORMAL al plano son (1, 0, -2).
Utilizando ese vector y el punto 0, 0, 0 podemos hallar la ecuación de la recta perpendicular al plano. La más utilizada es la paramétrica.
x=t
y=0
z=-2t
-
Alejandra
el 20/5/17
Hola buenos días, estoy estudiando dominios de funciones. Creo que en este ejercicio estoy siguiendo las reglas para los dominios, pero no me sale el resulado que pone en el libro. ¿Alguien me dice por qué? 
Victor
el 20/5/17Una raíz cuadrada tendrá resultado cuando en su interior exista un número positivo o cero.
Si en el numerador tienes un número negativo y en el denominador tienes un número negativo, el resultado de esa división será positiva, por lo que tendrá resultado.
En tu resolución tienes bien una parte, en la que dices que tendrá solución en un intervalo de (5/3, inf). Pero te falta calcular el intervalo para el que los valores del numerador y del denominador serán AMBOS negativos.
Te tiene que dar una solución final tal que Dom f = (-inf, -2] unión (5/3, inf).
Ten en cuenta que el valor x=-2 está incluido porque la raíz cuadrada de 0 es 0, y existe.
Alejandra
el 20/5/17 -
Paula Sánchez
el 20/5/17 -
Jose Lopez
el 20/5/17
No se como solucionar este ejercicio -
Paula Sánchez
el 20/5/17
No entiendo por qué los apartados a) b) e) f) g) h) i) son del tipo 1 elevado a infinito, si al sustituir el infinito da infinito entre infinito
Victor
el 20/5/17Si te fijas en los apartados a), b) y d), te queda siempre en el numerador y el denominador con x de mismo grado y con el mismo número multiplicando a las x. Por ejemplo, en el a es 4x/4x, en el b 3x/3x. El límite de 3x/3x va a darte 1.
En el apartado c) tienes 2x/x, ese límite cuando x tiende al infinito es 2.
2^infinito no es una indeterminación. Es infinito. -
ALOFRE
el 20/5/17Hola, podría alguien ayudarme con este problema?:
Un señor de 6 pies de altura se aleja a 5 pies/s de una farola de 15 pies de altura. Cuando está a 10 pies de ella:
- Calcule la velocidad de cambio de la longitud de la sombra.
- A que razón se mueve el extremo de su sombra?
Gracias!
-
Guillem de la Calle
el 20/5/17
