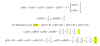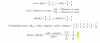-
Sandra
el 16/5/17 -
Eli
el 16/5/17 -
José Coteja
el 16/5/17 -
Guillem De La Calle Vicente
el 16/5/17
¿Por qué no hay un par de funciones distintas (g, h) donde h'=g y g'=-h que no sea (cos, sin)?
Este artículo (http://www.math.toronto.edu/mathnet/questionCorner/epii.html) dice:
También resulta que estas dos ecuaciones [dadas en negrita], junto con las condiciones g(0) = 1 y h(0) = 0 determinan [...] únicamente las funciones g y h.
¿Por qué es así?
David
el 19/5/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Guillem De La Calle Vicente
el 16/5/17Sea a un número real positivo. Demuestra por el contrarecíproco que si a <1, entonces a² <a.
David
el 19/5/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Guillem De La Calle Vicente
el 16/5/17 -
Matias
el 16/5/17Tengo otra duda con este ejercicio. Yo se que el lim de x tendiendo a 0 de sen(x)/x es 1, pero se puede extender a 2 variables? Les dejo un ejercicio que hice aplicandolo pero ahora me entro la duda si se puede hacer.
Gracias,saludos!
-
Matias
el 16/5/17Hola Unicoos, quisiera una mano con este ejercicio. Quisiera saber si con que el limite de la trayectoria en y=mx me de infinito, ya puedo decir que el limite no existe??
Gracias!
-
Guillem De La Calle Vicente
el 16/5/17 -
Facu Imfeld
el 16/5/17Duda de limites con 2 variables, ¿Cuántas direcciones debemos tomar para asegurar la existencia o no existencia del límite?
David
el 19/5/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
